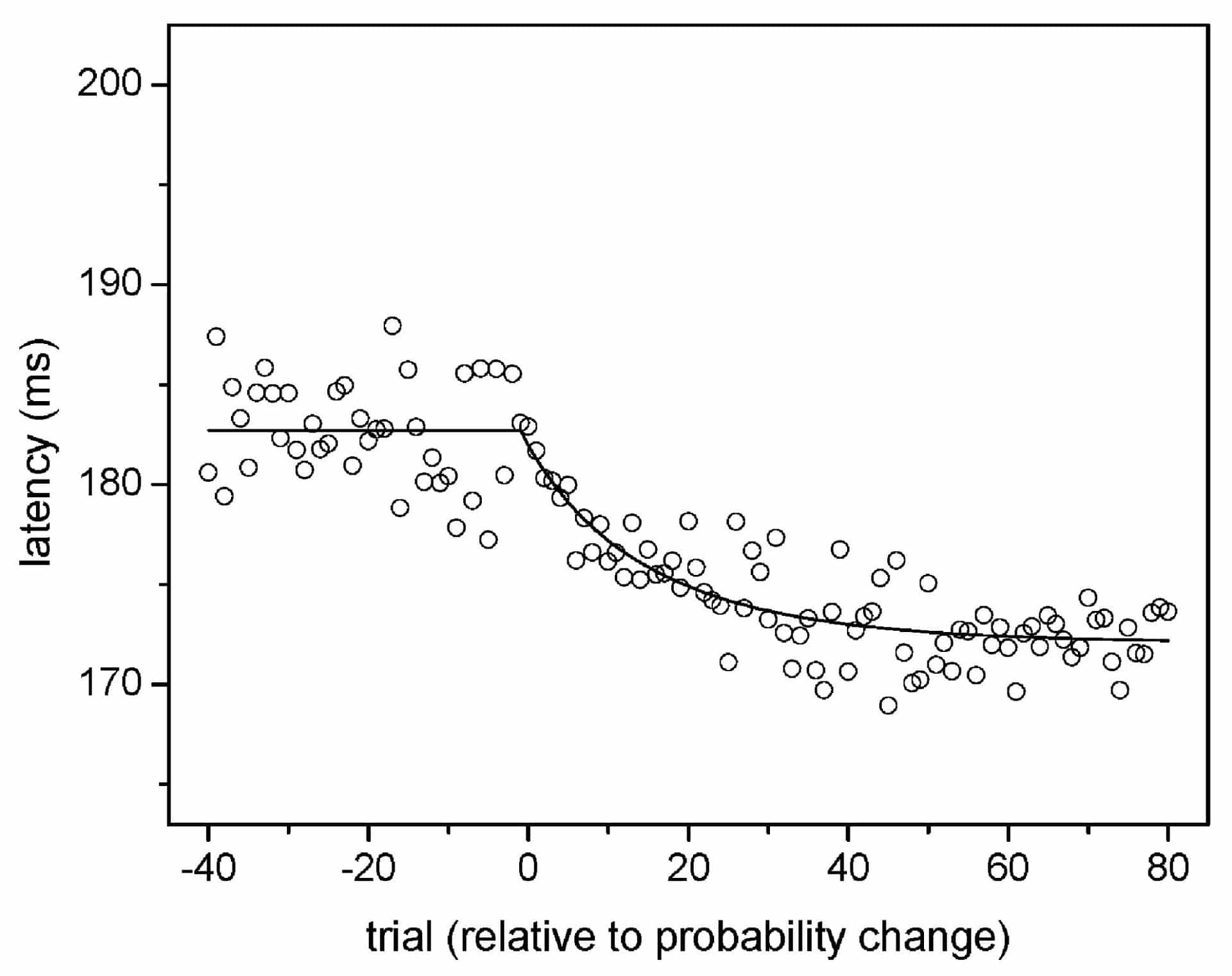
The median time to make an eye movement to a suddenly appearing target (saccadic latency) depends upon a subject’s expectation that the target will appear at a particular location. Previous work (Carpenter & Williams, 1995) found that, for fixed appearance probabilities, latency varies inversely with the log probability of a target’s appearance. If the target’s appearance probability changes, however, the subject’s expectation must change as well. We investigated the time course of this expectation change.

We measured saccadic latencies in human subjects for runs of 200 sequentially presented targets, altering the left/right appearance probabilities at a random point between 70 and 120 presentations. Initial left/right probabilities were 0.5/0.5, altering to 0.1/0.9, 0.33/0.67, 0.5/0.5, 0.67/0.33 or 0.9/0.1. Targets were yellow light emitting diodes (LEDs), spaced six degrees either side of a central fixation LED, that appeared 0.5 to 1.5 seconds after the onset of the fixation LED. A computer system (Carpenter, 1994) determined saccadic latencies from the output of an infrared oculometer. By performing repeated measurements, we determined average latencies for each presentation relative to the change in probability. The procedures complied with the Declaration of Helsinki, and were approved by the local ethics committee.

An abrupt change in appearance probability produced a continuous change in average saccadic latency that approached an asymptote (see Fig. 1). The continuous change commenced when the target probability changed, and was consistent with a ‘forgetful’ maximum-likelihood model that predicts:

p_x = (1-l{special})p_x-1 + l{special}q

where p_x is the subjective probability estimate (or expectation) after x presentations, (1-l{special}) is the relative weighting given to the prior estimate of probability, and q is the probability that the target appeared in the location on presentation x. Latency should then be proportional to a logarithmic transform of p_x. The constant l{special} represents the trade-off between responding quickly to true probability shifts and not responding to normal variation at a fixed probability level, and was approximately 0.05 for our data. This constant has potential implications for survival, for which an organism must distinguish true change in the environment from normal stochastic variation.