John McGuigan, James Kay & Hugh Elder
University of Glasgow, UK

https://doi.org/10.36866/pn.103.26

Ca²⁺ and, to a lesser extent, Mg²⁺ play crucial roles in the regulation of intracellular processes. The intracellular ionised calcium concentration ([Ca²⁺]) is in the nmolar range and the apparent constants (K^/) for Ca²⁺ and Mg²⁺ binding to intracellular ligands are in the nmolar and µmolar range respectively. These concentrations can be set by dilution but are bedevilled by contaminating concentrations of Ca²⁺/Mg²⁺, making buffers essential. The [X²⁺] in these buffers are either calculated or measured. Calculated values depend on the constants chosen and the method of computation and are so inconsistent, that until International Standards are available, the [X²⁺] in Ca²⁺/Mg²⁺ buffers have to be measured not calculated. Lacking International Standards, means there can be no exact measurements of intracellular [Ca²⁺] and the K^/ values for Ca²⁺/Mg²⁺ binding to intracellular ligands. This has repercussions for the modelling of intracellular Ca²⁺/Mg²⁺ regulation. International Standards are long overdue.

Ca²⁺/Mg² Buffers

The easiest way to make up solutions of such buffers is to use the ratio method with the appropriate background solution. In this method, two solutions of identical pH are made up; 1) an equimolar solution of Ca²⁺/Mg²⁺ and the ligand, and 2) a ligand solution. These are then mixed in various proportions ranging from 7:1 to 1:9 to give 10 buffer solutions, B1 to B10 (McGuigan et al., 2006). Making your own buffers has the advantage that their composition mimics the experimental conditions, but is time consuming. Calcium buffers in which the [Ca²⁺] are calculated are available from either WPI or ThermoFisher. Buying such buffers is convenient, but has the disadvantage that their composition may differ widely from the experimental solutions.

Concentration, activity and activity coefficients

In physiological solutions due to the interaction between the positive and negative ions, elevation of the boiling point and depression of the freezing point are less than would be expected from the salt concentrations. The salts in such solutions have thus an ‘effective concentration’ or activity, which is less than the actual concentration. The ratio of
activity/concentration is the mean activity coefficient (g±), mean, because it depends on both the cation and anions in the solution. However, in calculations it is often not the g±, but the single ion activity coefficients
(g+, g-) that are used; while the g± can be measured, the activity coefficient of a single ion cannot, and a convention has to be used to calculate it.

Calculation of [X²⁺] in the buffer solutions

Several papers describe how to calculate the [X²⁺] in buffer solutions, but the inherent problems in these calculations are often glossed over. As shown in McGuigan et al., (2016) there are four such problems.

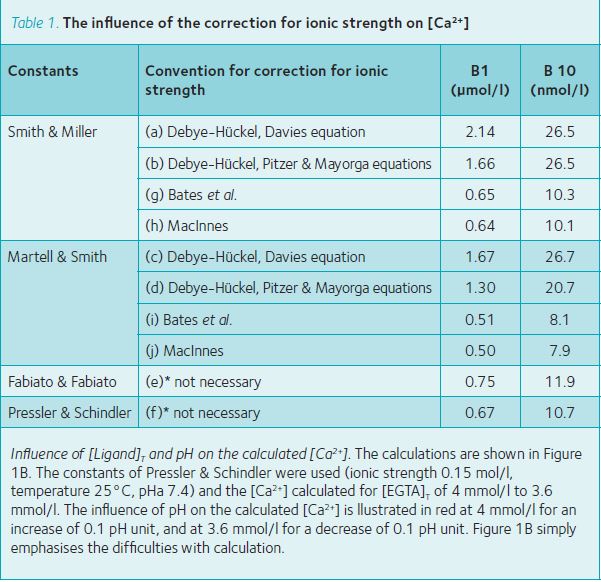
1. Tabulated constants for Ca²⁺/Mg²⁺ and H⁺ binding to Ca/Mg-ligands vary, and the choice of constants influences the calculated [X²⁺] values.
2. The constants have in many cases to be corrected for temperature and ionic strength. The data for temperature correction are not always available. 
3. The correction for ionic strength involves the calculation of the single ion activity coefficients for Ca²⁺, Mg²⁺, H⁺ and the ionic forms of the ligand. A common method to do this is to use the Davies equation to calculate the g± and the Debye-Hückel convention to calculate the single ion activity coefficient from this mean value. There are, however, other possibilities. The Debye-Hückel convention can be combined with the accurate equations of Pitzer & Mayorga, or the conventions of Bates et al. and MacInnes can be used; all give different results. pH is defined in terms of hydrogen activity, but the tabulated constants for Ca²⁺, Mg²⁺ and H⁺ binding to ligands are in terms of concentration, so measured pH_a (activity, [H⁺]g _H+ ) has to be converted to pH_c (concentration, [H⁺]) by using a convention to calculate the ion activity coefficient for H⁺-ions (gH⁺ ) . There is no defined way of doing this. An accurate conversion from pH_a to pH_c assumes that the potential of the reference electrode is the same in both the calibration solutions and the sample solution. This is usually not the case, and such changes can lead to deviations of ±0.1 pH units in the measured pH_a, which influences the calculated [X²⁺].
4. Due to absorbed water, ligands are not 100% pure, so purity has to be measured even if the [X²⁺] are calculated.

Results of calculation for the ionised concentrations in buffer solutions

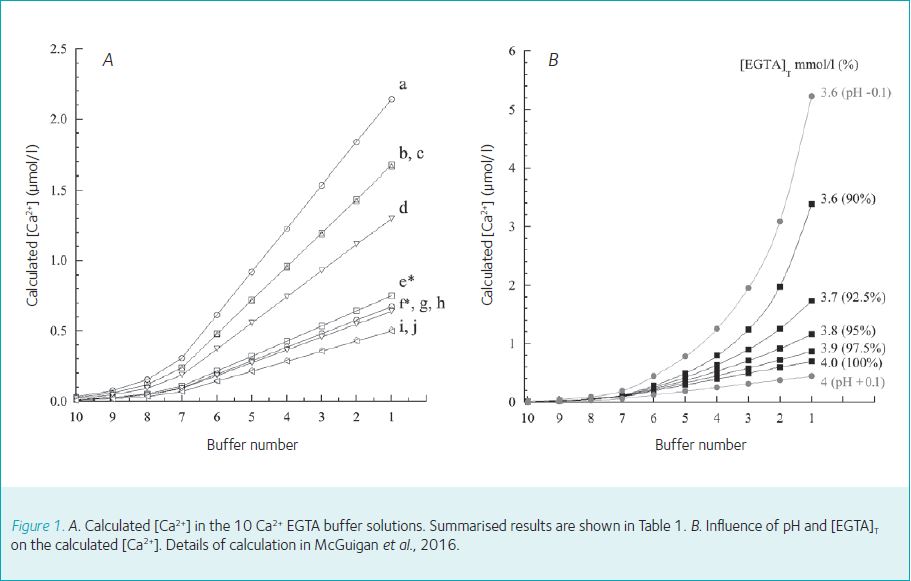
Ca²⁺ EGTA buffer solutions: These buffers are representative of the results of calculation for both Ca²⁺ /Mg²⁺ buffers.

Influence of constants and ionic strength corrections on the calculated [Ca²⁺]. The [Ca²⁺] in the 10 buffer solutions calculated with 4 sets of constants, corrected if necessary
to an ionic strength of 0.15 mmol/l, a temperature of 25°C and for a pH_a of 7.4, are illustrated in Figure 1A and Table 1. The most striking feature of Figure 1A is the variation in the calculated values for [Ca²⁺]; Table 1 shows the influence of the method of correction for the ionic strength on the calculated values and lists the actual [Ca²⁺] for buffer solution B1, and B10. The ratio maximum/minimum (curves a/j) for the calculated values was 4.3 for buffer solution B1 and 3.4 for buffer B10.

Software programmes for [Ca²⁺] and [Mg²⁺]

The [Ca²⁺]/[Mg²⁺] in buffer solutions can also be calculated using programs but these programs also suffer from exactly the same disadvantages as those of the calculations illustrated in Figure 1 (Figure 5B in McGuigan et al., 2016 for [Ca²⁺]).

Commercial Ca²⁺-buffers

These commercial buffers are based on calculated values and as illustrated in Figure 1A, if different constants were chosen, different values for [Ca²⁺] would be obtained. Moreover, these solutions are for an ionic strength for 0.1 mol/l, not the physiological ionic strength of 0.15 to 0.20 mol/l.

Consequences of calculated values

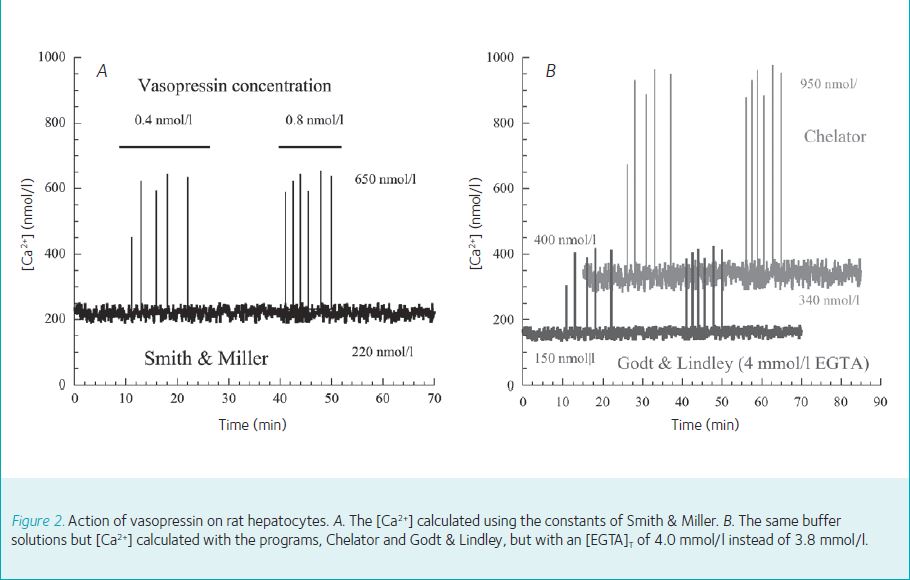
To illustrate the consequences of calculation on published [Ca²⁺] values, the action of vasopressin on intracellular [Ca²⁺] in liver cells is illustrated in Figure 2, based on experiments by Woods et al., (1987). In Figure 2A the [Ca²⁺] have been calculated using the values from Smith & Miller and the mean resting concentration for [Ca²⁺] was 220 nmol/l and the spikes reached a concentration of 650 nmol/l. However, as illustrated in Figure 2B, if the programs of Godt & Lindley (4 mmol/l EGTA) and Chelator are chosen the resting [Ca²⁺] varies from 150 nmol/l to 340 nmol/l and the spike amplitude from 400 nmol/l to 950 nmol/l.

Imagine such results in a clinical setting. The measured serum [K⁺] would be 3.4 mmol/l (hypokalaemia), 5.0 mmol/l (normal) or 7.7 mmol/l (hyperkalaemia) (Walker et al., 2014). The patient either requires an immediate infusion of K⁺, no treatment or is in danger of dying of K⁺ excess! It is an absurd situation, but it accurately describes the current situation for Ca²⁺ and Mg²⁺ buffers.

Measurement of [X²⁺] in buffer solutions

Criteria for measurement. Because of the problems with calculation, attempts have been made to measure the [X²⁺] in the buffer solutions. McGuigan et al., (2006) drew up a list of 6 criteria for the ideal method to measure [X²⁺] in Ca²⁺ and Mg²⁺ buffer solutions. Slightly modified and now including a 7^th criterion for independent verification they are:

1. Be applicable at the composition, temperature, ionic strength and pHa of the buffers
2. Should estimate both [Ligand]_T and the K^/
3. Should be applicable to both Ca²⁺ and Mg²⁺ buffers
4. Should not involve using listed constants
5. Should not involve converting from pH_a to pH_c
6. Using simulated data, the method should accurately estimate both [Ligand]_T and K^/
7. Should be independently verifiable

McGuigan et al., (2006) considered 7 different methods that have been used to measure the [X²⁺] but only one, the Ligand Optimisation Method (details in McGuigan et al., 2006, 2014, 2016; calculation software: jimkay99@virginmedia.com) met all these 7 criteria. The method is based on the measurements of [Ca²⁺]/[Mg²⁺] with a Ca²⁺ or Mg²⁺ electrode. The electrode characteristics, electrode slope and the constant of the recording system are initially determined in calibration solutions ranging from 0.5 mmol/l to 10 mmol/l (pX 3.301 to 2.000). Using these parameters, the pK^/ values and the [Ligand]_T in the 10 buffer solutions are then estimated using an iterative procedure.

Why International Standards for Ca²⁺ and Mg²⁺ buffers are necessary

As shown in Figures 1, calculated values for [Ca²⁺] in the buffer solution vary widely and it is similar for Mg²⁺ buffers (Figure 5A, McGuigan et al., 2016). The intracellular [Mg²⁺] is around 1 mmol/l, a concentration at which buffers are not required. However, estimations of intracellular [Mg²⁺] with ³¹P-NMR depends on the K^/ values for Mg²⁺ binding to ATP and related ligands whose estimation does require Mg²⁺ buffers. Since Intentional Standards do not exist, there is no way to determine which of the calculated values is correct, be it with spreadsheet, software programmes or commercial buffers. It is the classical ‘Catch 22’ situation.

Composition of International Standards for Ca²⁺ and Mg²⁺ buffers

That standards are necessary is beyond doubt, but the main question, and one that is still open to discussion, is the composition of such standards. Such buffers should have an ionic composition, ionic strength and pH similar to that of a physiological solution be it intracellular or extracellular, and be defined in terms of concentration not activity. To minimise the changes in potential at the reference electrode either a K⁺ (intracellular buffers) or Na⁺ (extracellular buffers) should be used instead of a 3 mol/l KCl reference.

Conclusions

Over the past 40 years the need for International Standards for Ca²⁺/Mg²⁺ buffers and the problems related to their lack, have simply been ignored. If there are no International Standards, there can be no exact determinations of intracellular [Ca²⁺], ³¹P-NMR estimations of [Mg²⁺] and of the K^/ values for intracellular binding of Ca²⁺/Mg²⁺ to physiological relevant ligands. Lacking accurate measurements of these parameters means that the results of modelling of the intracellular regulation of Ca²⁺ and Mg²⁺ have to be regarded with a degree of caution.

Finally, we conclude, that until International Standards are available, the [X²⁺] in Ca²⁺/Mg²⁺ buffers have to be measured not calculated. The only accurate way of doing this is to use the Ligand Optimisation Method (McGuigan et al., 2016).

References

McGuigan JAS, Kay JW & Elder HY (2006). Critical review of the methods used to measure the apparent dissociation constant and ligand purity in Ca²⁺ and Mg²⁺
buffer solutions. Prog Biophys Mol Biol 92, 333-370

McGuigan JAS, Kay JW & Elder HY (2014). An improvement to the ligand optimisation method (LOM) for measuring the apparent dissociation constant and ligand purity in Ca²⁺ and Mg²⁺ buffer solutions.
Prog Biophys Mol Biol 116, 203-211

McGuigan JAS, Kay JW & Elder HY (2016). Ionised concentrations in calcium and magnesium buffers: standards and precise measurement are mandatory. Prog Biophys Mol Biol Article in Press

Walker BR, Colledge NR, Ralston SH & Penman ID (2014). Davidson’s Principle and Practice of Medicine, 22^nd edition. Churchill Livingstone, Edinburgh

Woods NM, Cuthbertson KSR & Cobbold PH (1987) . Agonist-induced oscillations in cytoplasmic free calcium concentration in single rat hepatocytes.
Cell Calcium 8, 79-100