Can Ozan Tan (1,2) and J Andrew Taylor (1,2)

1: Department of Physical Medicine and Rehabilitation, Harvard Medical School, Boston, MA, USA
2: Cardiovascular Research Laboratory, Spaulding Rehabilitation Hospital, Boston, MA, USA

https://doi.org/10.36866/pn.77.25

Across a range of scales, from miles to inches, there can appear a form of self-similarity in structures that is quantifi able by fractal mathematics. It has been suggested that the natural occurrence of fractal structures is manifest in the similarity between the edge of a grain of sand and the edge of a coastline (Mandelbrot, 1982). Self-similarity is not an uncommon form and may have application to physiology. For example, fractal mathematics have been successfully employed to describe the branching patterns in the pulmonary vasculature (Lefèvre, 1983). However, recent advances in computing power and ready access to sophisticated mathematical software has allowed broader usage of fractal statistics to characterize a range of physiological patterns – including moment-to-moment changes in the heartbeat.

The applicability of fractals to cardiovascular signals was first suggested in the late 80s by Goldberger and colleagues. Since then, it has become popular to assess the fractal nature of beat-to-beat time series of heart period or arterial pressure. However, the idea of a ‘fractal’ time series is abstract; the fractal character of events that occur at discrete points in time is not readily observable. In contrast, when Mayer performed his experiments in rabbits almost two centuries ago, he observed a clearly distinguishable sinusoidal pattern in arterial pressure and theorized that this pattern relates to the physiological control of the cardiovascular system. As a (perhaps indirect) consequence, the effort to quantify and characterize heart period and arterial pressure variability has been most focused on spectral analysis. However, moving beyond the spectral domain and into the fractal domain may not be warranted. Indeed, as Steven Krantz, in his 1989 critique to Mandelbrot said “the trouble with any subject that relies more on computer output than on theory is that one has to think of something to say about it.” (Krantz, 1989)

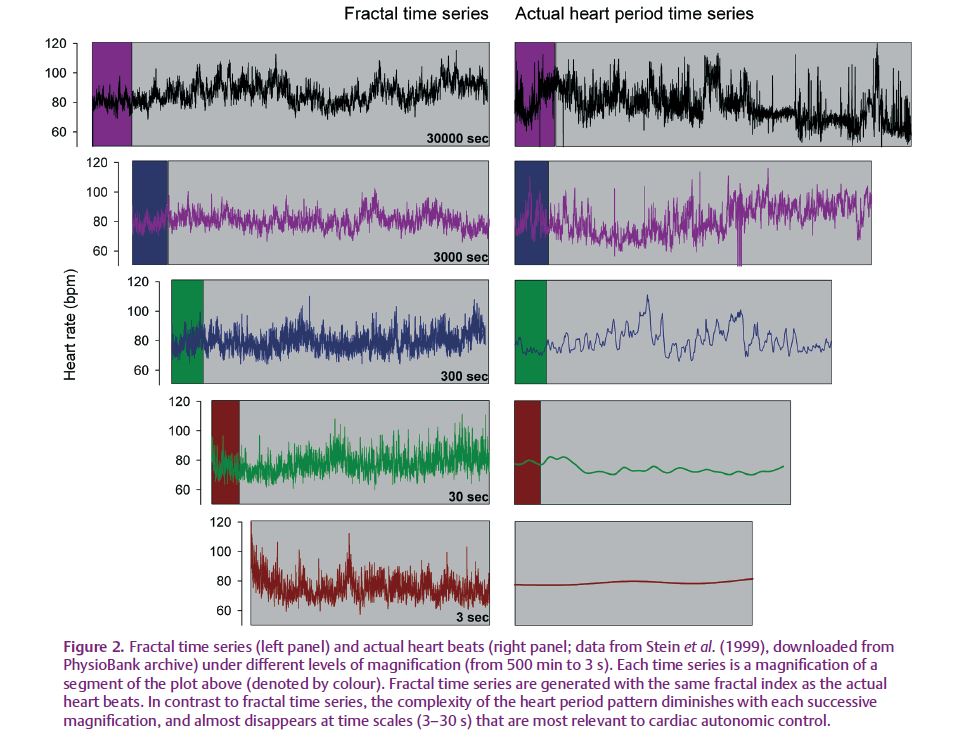
What does it mean to be fractal? According to the simplest definition, fractal objects are similar at all levels of magnification, displaying an inherent property of self-similarity that is infinitely complex (see Fig. 1). Therefore, if heart period is fractal, it must fluctuate with infinitely long as well as infinitesimally small periods, each having a similar pattern. However, by definition, heart beats are discrete events; as such, the resolution of the structure is limited and can be no smaller than the shortest interval between consecutive beats. In fact, partly because the heart beat is discrete, the complexity of the heart period pattern is diminished with each successive magnification (Fig. 2). Nevertheless, if we assume that heart period does display self-similarity and is infinitely complex, what would that mean physiologically? Are fluctuations in the heart beat with a period of 3 s (approximately the length of a breath) or 33 years (close to half the human life span) both relevant to cardiac autonomic control? Certainly not. Spectral analysis of cardiovascular time series suggests that fast fluctuations in heart rate period (around 6 s and faster) are primarily related to cardiac vagal control, whereas slower fluctuations (around 6–20 s) may reflect both vagal and sympathetic modulation. (It must be noted, though, that the use of spectral analysis to characterize cardiac autonomic control is still under debate; Parati et al. 2006; Taylor & Studinger, 2006.) Therefore, fluctuations in heart period, induced by autonomic outflow, appear to have a relatively restricted temporal range. So, could the fractal properties of heart period still provide unique insight to the underlying physiology? One answer was eloquently provided by Francis et al. (2002): the fractal scaling exponent “should not be considered to be a unique cardiovascular indicator in a separate ‘fractal’ class from conventional power-spectral analysis, because it has a clear and comprehensible grounding in spectral analysis.” Thus, the analysis of patterns in cardiovascular time series need not move beyond the spectral domain into the fractal domain.

The application of fractals to heart beat time series assumes that these time series can be defined as fractal processes and that changes in them reflect changes in cardiac control. This assumption arises from anecdotal reports that fractal behaviour could be inferred based on noisy spectrograms and that cardiac disease produced a less noisy spectrogram. However, if the ‘trajectory’ of the heart period time series seems “more like a strange attractor than like the periodic attractor characteristic of truly regular processes” (Goldberger et al. 1990), adequate mathematical testing should be employed to determine the actual presence of the pattern. Instead, power-law (1/f) scaling of the power spectral density which can be indicative of a self-similar structure is commonly taken as evidence for fractal behaviour. However, power-law scaling and self-similarity are not sufficient to define truly fractal behaviour (Avnir et al. 1998). (A straight Euclidean line is technically self-similar, but obviously not fractal.) Indeed, we have recently shown that despite a strong power-law scaling, a majority of heart period time series in healthy young subjects do not conform to the assumed standard fractal model and therefore cannot be considered fractal processes (Tan et al. 2009). If this is true across the range of human health and disease, fractal estimates produce completely meaningless and irreproducible values.

Perhaps because of their unreliability, fractal estimates of heart period variability have no identifiable value that could be considered ‘normal’. Fractal estimates can range from 0, reflecting a so-called fractal Gaussian pattern, to 2, reflecting a fractal Brownian pattern. These two are highly distinct; one is stationary and the other is not. Despite the obvious discrepancies in finding both of these patterns, the recent literature reports values as low as 0.7 and as high as 1.2 for healthy young subjects (Struzik et al. 2004; Mourot et al. 2007). Moreover, very large variability can be observed even under the exact same experimental conditions (Tan et al. 2009); estimated fractal indices can range from ~0.5 to ~1.4 for healthy individuals during supine rest (Heffernan et al. 2008). To put this range in perspective, these are values that have been reported to represent cardiac control in cyclists during heavy exercise (~0.5; Casties et al. 2006) and to reflect the absence of cardiac control in human heart failure (~1.3; Goldberger et al. 2002).

Lastly, it might be worthwhile to consider the raison d’etre for potential fractal behaviour in heart period variability. It has been theorized that the absence of a characteristic time scale (a la fractal fluctuations) facilitates the functional adaptive capacity of the cardiovascular system by helping to prevent ‘excessive mode locking.’ This would be along the lines of pervasive oscillations present in some pathological conditions, such as in heart failure (Peng et al. 1993). Improved adaptive capacity via fractal patterns is, in fact, a plausible theory, and could well be true. However, the presence of random noise (which abounds in biological systems) can serve exactly the same purpose; the contribution of a fractal, scale-independent mechanism is not crucial. Therefore, it is incumbent upon the theorizer to unambiguously define the presence of a fractal pattern versus simple
random noise.

More than two decades ago, when it was first proposed that the heart period is fractal, it was suggested that physiology may prove to be a rich source for the study of fractals as well as other types of non-linear dynamics (Goldberger et al. 1990). However, exploration of fractals should avoid being self-referential, generating “pictures to learn more about the pictures” (Krantz, 1989). Although application of sophisticated analyses to cardiovascular data can lead to deeper understanding, it also has the potential to cloud our view of the physiology.

References

Avnir D, Biham O, Lidar D & Malcai O (1998). Is the geometry of nature fractal. Science 279, 39–40.

Casties JF, Mottet D & Le GD (2006). Non-linear analyses of heart rate variability during heavy exercise and recovery in cyclists. Int J Sports Med 27, 780–785.

Francis DP, Willson K, Georgiadou P, Wensel R, Davies LC, Coats A & Piepoli M (2002). Physiological basis of fractal complexity properties of heart rate variability in man. J Physiol 542, 619–629.

Goldberger AL, Amaral LA, Hausdorff JM, Ivanov PC, Peng CK & Stanley HE (2002). Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci U S A 99, 2466–2472.

Goldberger AL, Rigney DR & West BJ (1990). Chaos and fractals in human physiology. Sci Am 262, 42–49.

Heffernan KS, Sosnoff JJ, Fahs CA, Shinsako KK, Jae SY & Fernhall B (2008). Fractal scaling properties of heart rate dynamics following resistance exercise training. J Appl Physiol 105, 109–113.

Krantz SG (1989). Fractal geometry. Math Intell 11, 12–16.

Lefèvre J (1983). Teleonomical optimization of a fractal model of the pulmonary arterial bed. J Theor Biol 102, 225–248.

Mandelbrot B (1982). The Fractal Geometry of Nature. WH Freeman and Co., New York, NY.

Mourot L, Bouhaddi M, Gandelin E, Cappelle S, Nguyen NU, Wolf JP, Rouillon JD, Hughson R & Regnard J (2007). Conditions of autonomic reciprocal interplay versus autonomic co-activation: effects on non-linear heart rate dynamics. Auton Neurosci 137, 27–36.

Parati G, Mancia G, Di RM & Castiglioni P (2006). Point: cardiovascular variability is/is not an index of autonomic control of circulation. J Appl Physiol 101, 676–678.

Peng CK, Mietus J, Haussdorf JM, Havlin S, Stanley HE & Goldberger AL (1993). Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys Rev Lett 70, 1343–1349.

Stein PK, Ehsani AA, Domitrovich PP, Kleiger RE & Rottman JN (1999). Effect of exercise training on heart rate variability in healthy older adults. Am Heart J 138, 567–576.

Struzik ZR, Hayano J, Sakata S, Kwak S & Yamamoto Y (2004). 1/f scaling in heart rate requires antagonistic autonomic control. Phys Rev E Stat Nonlin Soft Matter Phys 70, 050901.

Tan CO, Cohen MA, Eckberg DL & Taylor JA (2009). Fractal properties of human heart period variability: physiological and methodological implications. J Physiol 587, 3929–3941. http://jp.physoc.org/content/587/15/3929. long

Taylor JA & Studinger P (2006). Counterpoint: cardiovascular variability is not an index of autonomic control of the circulation. J Appl Physiol 101, 678–681.