Emanuel Azizi and Thomas J Roberts
Brown University, Department of Ecology and Evolutionary Biology, Providence, RI, USA

https://doi.org/10.36866/pn.77.28

The forces generated by the contractile machinery of skeletal muscle are transmitted to the skeleton through tendons. Most tendons don’t simply transmit forces but rather behave like springs, stretching as muscular forces are applied and recoiling as forces decline. The significance of tendon elasticity is most obvious in cyclical movements where elastic energy can be stored and recovered with tremendous efficiency thereby lowering the energetic cost of movement. An extreme example of this mechanism is the bouncy gaits of hopping wallabies, where it has been shown that tendon stretch and recoil can allow the organism to recycle nearly all of the energy from a previous stride (Biewener & Baudinette, 1995). This elastic behaviour of tendons extends well beyond such obviously bouncy gaits and also increases the energetic economy of walking and running.

As a biological spring, the capacity of a tendon for storing elastic energy is largely determined by its stiffness. The mechanical energy stored in tendons is a function of the force applied to the tendon and length changes the tendon undergoes in response to that load. This relationship simplifies biomechanical models, where energy storage can be calculated from the modelled muscle force and a tendon’s characteristic stiffness (Zajac, 1989). This approach assumes that a given tendon is governed by a single relationship between force and length that defines a single stiffness. In situ measurements of isolated tendons suggest that this assumption is valid for so-called ‘free’ tendons, such as the Achilles, that span a gap between muscle and bone (Fig. 1).

However, free tendons are not the only elastic structures capable of storing elastic energy. In many muscles the free tendon is continuous with broad sheet-like tendons, or aponeuroses, that function as the attachment and insertion sites for muscle fibres (Fig. 1). Both tendons and aponeuroses consist of collagen bundles oriented primarily along the muscle’s line of action embedded in an extra-cellular matrix. In fact, the same collagen bundle may extend from the tendon to the aponeurosis with no structural separation. These shared structural features have been used to infer functional similarity between tendons and aponeuroses. It is commonly assumed that the stiffness of an aponeurosis is the same as that of the free tendon, though some recent measurements challenge this assumption (e.g. Magnusson et al. 2003).

Although aponeuroses share some structural similarities with free tendons, they probably undergo a more complex loading regime. Many aponeuroses cover a substantial portion of the muscle belly (Fig. 1). It is well accepted that when muscles contract and fibres shorten, the muscle expands in other dimensions to maintain a constant volume. The image of a flexing bodybuilder is a familiar reminder that muscles change shape when they contract. Given the close association of aponeuroses with the muscle belly, it is reasonable to predict that shape changes in a contracting muscle may also deform the aponeurosis along multiple axes.

In a recent paper we used high-speed fluoroscopy to characterize three-dimensional deformations in aponeuroses during muscle contraction (Azizi & Roberts, 2009). Our measurements confirmed that aponeuroses are stretched both parallel and perpendicular to a muscle’s line of action during muscle contraction. This pattern of stretch indicates that the aponeurosis is loaded biaxially.

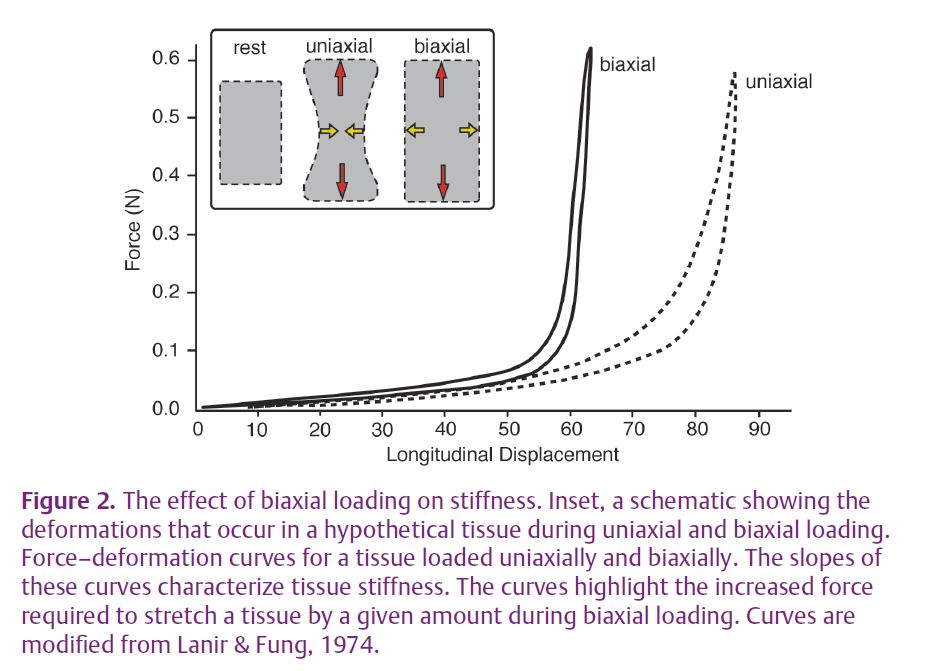
To appreciate the functional significance of biaxial loading, consider a case where the tissue is only loaded in one direction. When loaded uniaxially any solid material will tend to get thinner in directions perpendicular to the line of pull; a stretched rubber band displays a characteristic ‘necking’ where it shortens perpendicular to the direction of loading (Fig. 2). In contrast, under biaxial loading the tissue is prevented from shortening, and with enough loading can be stretched in two dimensions. Biaxial loading requires more force for a given stretch (Fig. 2). What this means for muscle is that the effective stiffness of the tendon spring is greater in the longitudinal direction than would be expected for uniaxial loading (Fig. 2).

We were able to test the idea that biaxial loading increases the effective stiffness of aponeurosis by comparing the aponeurosis stiffness during active and passive force production. When the muscle was loaded passively (by stretching it to long lengths), the aponeurosis shortened in the orthogonal direction, as expected for uniaxial loading (Fig. 3). The stiffness measured under these conditions was significantly lower than the stiffness measured for biaxial loading during active force production (Fig. 3).

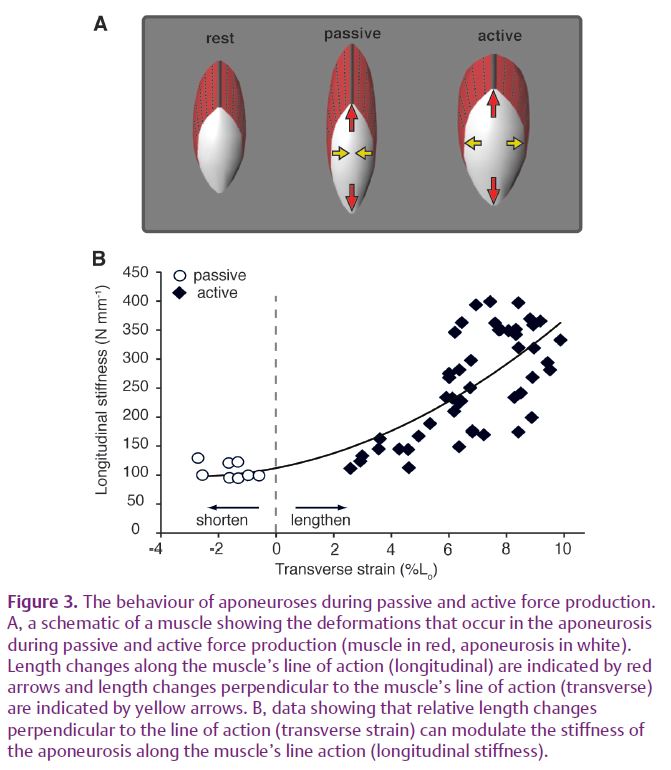
The effects of biaxial loading may explain previously published results that were considered difficult to reconcile with a model of the aponeurosis as a uniaxially loaded spring. Measurements on isolated muscles found the stiffness of the aponeurosis along the muscle’s line of action increases substantially in active as compared with passive force production (Zuurbier et al. 1994; Lieber et al. 2000). Such changes in aponeurosis stiffness were difficult to explain when only deformations along the muscle’s line of action were considered. However, when one considers the length changes that occur orthogonal to the muscle’s line of action, it becomes clear that biaxial loading provides a likely mechanism for stiffness modulation in aponeuroses (Fig. 3).

Variable stiffness in aponeuroses may have important implications for movement. The use of stiffness values based on uniaxial material properties may underestimate the elastic energy stored in aponeuroses during active contractions. Variable stiffness may also have implications for motor control. If the muscle ‘sees’ a different spring stiffness under different conditions, the motor control system must accommodate this variability. The degree to which changes in aponeurosis stiffness are tuned to the mechanical demands of movement remain unknown and should provide fertile ground for future studies.

References

Azizi E & Roberts TJ (2009). Biaxial strain and variable stiffness in aponeuroses. J Physiol 587, 4309–4318. http://jp.physoc.org/content/587/17/4309.long

Biewener AA & Baudinette RV (1995). In vivo muscle force and elastic energy storage during steady-speed hopping of tammar wallabies
(Macropus eugenii). J Exp Biol 198, 1829–1841.

Lanir Y & Fung YC (1974). Two-dimensional mechanical properties of rabbit skin. II. Experimental results. J Biomech 7, 171–182.

Lieber RL, Leonard ME & Brown-Maupin CG (2000). Effects of muscle contraction on the load-strain properties of frog aponeurosis and tendon. Cells Tissues Organs 166, 48–54.

Magnusson SP, Hansen P, Aagaard P, Brond J, Dyhre-Poulsen P, Bojsen-Moller J & Kjaer M (2003). Differential strain patterns of the human gastrocnemius aponeurosis and free tendon, in vivo. Acta Physiol Scand 177, 185–195.

Zajac FE (1989). Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng 17, 359–411.

Zuurbier CJ, Everard AJ, Vanderwees P & Huijing PA (1994). Length-force characteristics of the aponeurosis in the passive and active muscle condition and in the isolated condition. J Biomech 27, 445–453.

Acknowledgements

The authors would like to acknowledge support from the United States National Institute of Health grants AR055295 to T.J.R. and AR054246 to E.A., as well as the W.M. Keck Foundation.