James A Fraser & Christopher L-H Huang
Department of Physiology, University of Cambridge, Cambridge, UK

https://doi.org/10.36866/pn.58.21

A reader might justifiably believe that the mechanisms that determine the resting volumes (Vc) and membrane potentials (Em) of animal cells were clarified long ago. Cell volume maintenance is understood to require sodium (Na+) pump activity to exclude Na+, which then balances the osmotic effect of intracellular proteins (Guyton & Hall, 2000). Em at equilibrium may be calculated accurately, using Mullins and Noda’s (1963) elegant modification of the Goldman-Hodgkin-Katz equation (Hodgkin & Katz, 1949). Numerous well-characterized processes alter Vc and Em from their resting states. For example, depolarization of Em occurs due to increased Na+ permeability during action potentials, while most cell types show Vc regulation in response to volume changes and all must change their resting Vc during e.g. differentiation and mitosis (review: Lang et al. 1998).

So what remains to be understood? Em and Vc are dependent on similar mechanisms, particularly Na+ pump activity, and it is not clear how their steady state values are determined. For example, what mechanisms of control of Na+ pump activity are necessary to achieve stable values of Vc and Em?Furthermore, what mechanisms could regulate Vc and Em independently in processes such as muscle hypertrophy, when Vc changes and most recognised mechanisms of Vc regulation necessarily alter the intracellular ion concentrations that determine Em (Ferenczi et al. 2004)?

In The Journal of Physiology, we recently (Fraser & Huang, 2004) formulated a limiting relationship between steady state Vc and Em (Box 1). However, full investigation of Vc and Em determaination required the development of a formal model. Its principal innovation was the calculation of Em directly from the intracellular charge difference and membrane capacitance, thus avoiding the equilibrium assumptions implicit in Goldman-Hodgkin-Katz type equations. The influence of transmembrane ion fluxes and Vc changes upon Em could then be modelled directly from the resultant changes in precise intracellular ion concentrations, allowing inclusion of essentially any quantifiable process in the model, including the activity of the Na+ pump and its electrogenic influence (Hernandez & Chifflet, 2000).

BOX 1 Constraints upon steady state Vc and Em in animal cells

(1) Intracellular and extracellular osmolarity are equal: [Na+]i + [K+]i + [Cl–]i + [X–]i = ∏e
(2) There is gross charge neutrality inside the cell: [Na+]i + [K+]i – [Cl–]i + zX[X–]i ≈ 0
(3) Cl- is passively distributed across the cell membrane.

Thus steady-state Vc and Em are related:

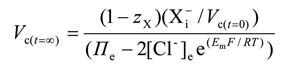
where: square brackets [ ] denote concentrations; subscripts e and i denote extracellular and intracellular respectively; t=00 denotes initial (disequilibrium) conditions; t=∞ denotes steady state conditions; Vc = cell volume; X­membrane-impermeant anions; zX mean charge valency of X -; ∏e total extracellular osmolarity; Em resting membrane potential; F Faraday’s constant; R the gas constant; and T the absolute temperature.

Figure 1 demonstrates the principal conclusion of this work: Vc and Em converge to unique set-points without requiring any explicitly Vc– or Em­sensitive mechanisms. However, the existence of stable points of Vc and Em requires the presence of membrane­impermeant intracellular ions (X-i) as well as a functional sodium pump. Given the constraints detailed in Box 1, consider the (physiological) situation where Cl- is the major extracellular anion. X-i then prevents Cl- from achieving chemical equilibrium ([Cl-]i = [Cl-]e) across the cell membrane. In the absence of sodium pump activity, the inward Cl- gradient would result in an unopposed Cl- influx, permitting a cation influx and cell swelling until X-i was infinitely diluted. Conversely, in the absence of X-i, Na+ pump activity would cause cell shrinkage indefinitely. Each pump cycle decreases [Na+]i and increases [K+]i, creating an outward K+ gradient. Efflux of K+ then results in hyperpolarization of the cell, thereby promoting Cl- efflux which “short-circuits” the K+ potential and shrinks the cell. When Cl – is the only intracellular anion, [Cl-]i must always be half the total intracellular ion concentration, despite such a reduction in its cellular content, so cell shrinkage could continue indefinitely and significant polarization of the membrane would be impossible. This would not occur in the presence of X-i: [Cl-]i reduction is then possible as shrinkage increases [X-]i, so that eventually K+ efflux cannot drive Cl ­efflux, and instead causes Em polarization that then opposes further K+ efflux. Together, then, the tendency of X-i to make the cell swell and the tendency of the sodium pump to make it shrink can, at one single point, reach a precise balance. It was thus shown that Vc was linearly related to X-i content (Fig. 1).

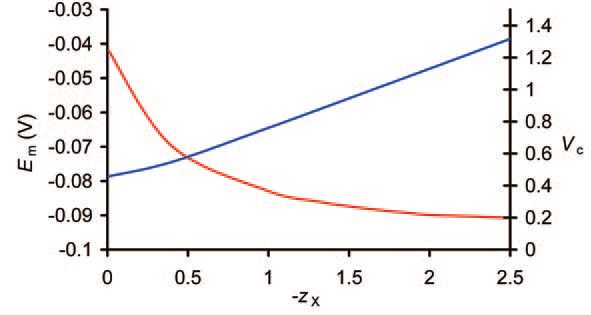
However, this linear relationship implies that the steady-state concentration of X-, and hence the value of Em, is then independent of X-i content. However, as shown in Fig. 2, the mean charge valency of X – (zX) does influence Em as well as Vc. If (-zX)<<1,[X-]i must be higher than [K+]i to achieve gross charge neutrality, whereas if (-zX)>>1, [K+]i could significantly exceed [X-]i. As intracellular and extracellular osmolarity must remain equal, greater zx magnitudes are required for higher [K+]i and hence more polarized Em. Thus the previously overlooked parameter zX is critical to determination of Em and Vc.

This analysis (Fraser & Huang, 2004) thus identifies and characterizes the factors that determine Vc and Em and the relationship between them. In excitable cells at least, Na+ pump density above a critical value little influences either Vc or Em as it operates close to its energetic limits at steady state. Instead, for given transmembrane ion permeabilities, steady-state Vc is determined by X-i content and zX, while Em is determined solely by zX. Charge­ difference modelling thus proved a powerful tool, permitting investigation of the many mechanisms that determine, maintain and regulate Vc and Em.

References

Ferenczi EA, Fraser JA, Chawla S, Skepper JN, Schwiening CJ & Huang CL-H (2004). Membrane potential stabilization in amphibian skeletal muscle fibres in hypertonic solutions. J Physiol 555, 423­438.

Fraser JA & Huang CL-H (2004). A quantitative analysis of cell volume and resting potential determination and regulation in excitable cells. J Physiol 559, 459-478.

Guyton AC & Hall JE (2000). Textbook of Medical Physiology (10th Ed.). NY, Saunders.

Hernandez JA & Chifflet S (2000). Electrogenic properties of the sodium pump in a dynamic model of membrane transport. J Membr Biol 176, 41-52.

Hodgkin AL & Katz B (1949). The effect of sodium ions on the electrical activity of the giant squid axon. J Physiol 108, 37-77.

Lang F, Busch GL, Ritter M, Volkl H, Waldegger S, Gulbins E & Haussinger D (1998). Functional significance of cell volume regulatory mechanisms. Physiol Rev 78, 247-306.

Mullins LJ & Noda K (1963). The influence of sodium-free solutions on the membrane potential of frog muscle fibers. J Gen Physiol 47, 117-132.