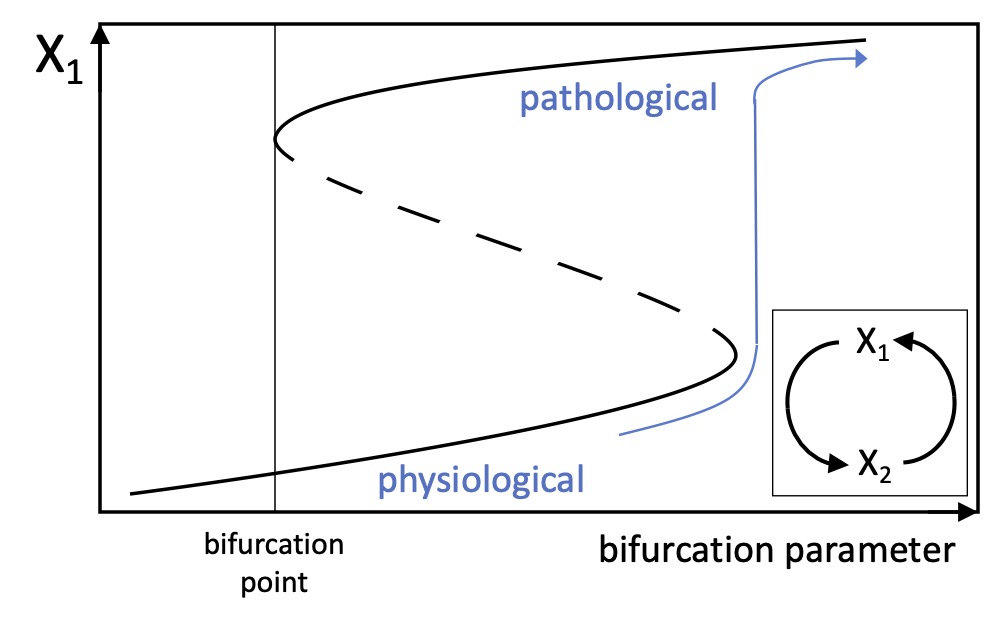
It has been proved that different life processes can be modeled in terms of the dynamics of positive loop systems, i.e. closed chains of interactions with an even number of inhibitory steps, or none. These processes include regulatory mechanisms of gene expression, and cellular activities like division, differentiation, and migration. A generalization of this complex of evidence has led to the Loopomics paradigm, which assumes that all functional elements of a living being are involved in variously connected loop systems [1]. This allows to assume that the whole organism is governed by a restricted set of rules, which nevertheless give rise to a multitude of highly diverse epiphenomena, collectively known as biodiversity (cells, tissues, organisms, etc.). Accordingly, any change occurring in a living being can be reconducted to the activity of a multistable positive loop system switching among different steady states [2]. This is extremely relevant in pathophysiology, as the insurgence of a disease in a healthy organism starts from a primary event that converts the system from a physiological to a pathological status. Bistable switches have been actually used to describe different diseases, including immunological disorders, neurodegenerative and neurological problems, infections, and cancer [3, 4].      Hence, a wide set of data argues for a new theory, based on the idea that any disease affecting a healthy human involves a change that can be reconducted to the activity of a positive loop generating a multistable system, typically a bistable one. In this kind of systems, the transition from monostability to multistability can be driven by the variation of bifurcation parameters, allowing the system to switch from a “physiological” to a “pathological” steady state. An exemplificative representation (Figure 1) shows a bifurcation diagram of a positive loop (inset) describing a schematic pathogenic process involving two functional agents, X1 and X2, which may represent cells (e.g. lymphocytes), enzymes (e.g. kinases), or signal molecules (e.g. interleukins). The diagram shows the trajectories of the steady states of X1 as a function of a bifurcation parameter, where continuous branches represent stable equilibrium points and the dashed branch unstable equilibrium points. The arrow indicates a possible path followed by the system in the transition from physiological to pathological status.  The system dynamics are characterized by hysteresis, thereby opening the possibility of irreversible transitions for a strengthening of the interactions among the loop functional agents.      This theory assumes that the huge diversity of pathologies that can possibly affect a healthy human can be reduced to a unique theoretical model, consisting of a positive loop system representing functional relationships among cells, molecules, or biochemical agents. In this context, the physical entities that correspond to bifurcation parameters should be considered best therapeutic targets aiming at achieving full control of the disease mechanisms. The application of this new idea to pathophysiological studies could lead to overcome the disappointing impasse that is currently characterizing many approaches to unsolved diseases. Recent models of neurological diseases could provide a basis for a validation of the theory [5].