Everything comes in cycles

Richard Naftalin considers problems relating to primary and secondary active transport

Features

Richard Naftalin
King’s College London, London, UK

---

https://doi.org/10.36866/pn.67.14

In the 1950s and 60s there were still revanchist arguments about whether active transport existed at all! Gilbert Ling believed that protoplasm had specific adsorptive properties with stereoselectivity for K+ over Na+ that explained the asymmetric ion distribution in cells without any need to invoke an energy-consuming process (Ling & Ochsenfeld, 1976) However active transport of Na+ across frog skin was unequivocally demonstrated by Ussing (Ussing & Zerahn, 1951).

E J Harris, my mentor in the Biophysics Department at University College London, was one of the first to show that Na+ is pumped out of muscle via an energy-consuming process (Edwards & Harris, 1957; Harris. 1957). Post & Jolly (1957) also showed that ion distributions across the cell membranes depended on an energy-consuming process. This work stimulated Skou to characterise the sodium pump as an ATPase enzyme, which underwent reversible phosphorylation (Skou, 1998). Ron Whittam’s (Whittam & Ager, 1964; 1965) and Garrahan & Glynn’s (1967) demonstration that active movements of Na+ and K+ are coupled stoichiometrically to ATP breakdown and running the pump backwards produced net ATP synthesis (Lew, Glynn & Ellory. 1970) consigned the Na+-K+-ATPase pump, firmly into the conceptual camp of an enzymatic
‘mechanical’ carrier protein for three decades.

Peter Mitchell, the inventor of chemiosmotic theory, put the dilemma of coupling of proton flow to ATP synthesis very well in his review paper (Mitchell, 1977). He wrote that the consensus view of energy transformations in the 1950-60s was in terms of chemical group transfer reactions, as with substrate level phosphorylation of ATP; so the bioenergetics people were looking for ‘a chemical intermediate’ which could explain chemical transduction of electron and proton transport with ATP synthesis. Mitchell’s hypothesis, which stated that no such intermediate existed and that the energy transformation was the result of coupling of the proton electrochemical potential gradient to the ATP synthetic process, was quite revolutionary and was met with varying degrees of incredulity. One of the problems then was that there was no concrete proof – just a diagram! This omission was set to rights by Boyer’s and Walker’s structural solution of the ATP synthase (Boyer, 1997; Stock et al. 2000).

Coupled transport became the physiological zeitgeist of the late 60s. Robert Crane’s view that sugars were transported up their concentration gradient, as a result of energy transduced from a Na+ gradient across intestinal brush borders, was readily accepted, perhaps as a result of Mitchell’s efforts (Crane, 1962). The apotheosis of Crane’s work came about 10 years later with the unequivocal demonstration, using brush border membrane vesicles, that the only source of energy for uphill sugar accumulation was the electrochemical gradient of Na+ across the membrane (Murer & Hopfer, 1974).

Another important example of coupling of flows was the demonstration that water flows are coupled to net Na+ movement in intestinal epithelia, as a consequence of osmotic coupling resulting from active Na+ accumulation into a ‘central compartment’ (Curran 1960), later located in the extracellular and lateral intercellular spaces.

The other important strand to understanding of coupled flows in biology came from theoretical work on irreversible thermodynamics as applied to biological flows (Kedem & Katchalsky, 1961). Two important aspects of their work have not been fully assimilated. They recognized that coupling of flows across biological membranes, as in artificial membranes, arises from frictional interactions between the flowing components within the membrane. Coupling between separate molecules is not the result of static ‘thermodynamic’ interactions, as where electrical and chemical potentials generate a combined electrochemical potential within a single ion. This goes against the grain of current thinking, which assumes that the cotransported molecules are yoked together by the carrier within the membrane phase, so that their separate thermodynamic potentials merge stoichiometrically to generate a multicharged complex whose single electrochemical potential generates coupled solute flows across the membrane.

Problem with primary active transport

A second important aspect of irreversible thermodynamic theory is the recognition that the scalar (non-vectorial) nature of the energy dissipation from chemical reactions, such as ATP hydrolysis, must be transformed into a vectorial force to generate vectorial ion flow (Kedem, 1961). All the circulating carrier models of active transport by P-type ATPases, are presumed to impart concentrative energy to the transported ligand by the agency of the protein levering, via ATP-dependent alterations in the relative affinities of Na+ and K+, the bound ligands between the E1 and E2 states of the enzyme. This is presumed to transform the scalar energy of ATP hydrolysis to a vector force generating concentration work between the intra and extracellular solutions (Jardetzky, 1966; Lauger, 1984; Apell, 2004; Artigas & Gadsby, 2006).

Although the affinity ratio of the carrier for Na+ and K+ is changed from 28 to 710 by raising ATP from 0.1 to 4mM (Homereda et al. 1991) this only represents energy transferred to the carrier protein itself and not to the mobile ligands.

It has become apparent that the two gates enclosing the central occlusive compartment of the Na+- K+-ATPase can open simultaneously during the normal pump cycle (Apell 2004; Artigas & Gadsby 2006). Thus, the hypothesis that ions contained within the central compartment are prevented from running down their concentration gradients by fixed mechanical properties of the gates is no longer tenable. If the chemical reaction only transfers energy to the transporter to alter its gating properties and affinities towards the transported ligands, this will not raise the kT energy of ligands within the occluded central cage to permit further isoergonic transfer from the central compartment to the higher energy state of ions within the trans solution. A pore pump model incorporating direct energy transference from ATP hydrolysis to increase ionic motion out of the central occlusion site is required (Fig. 1).

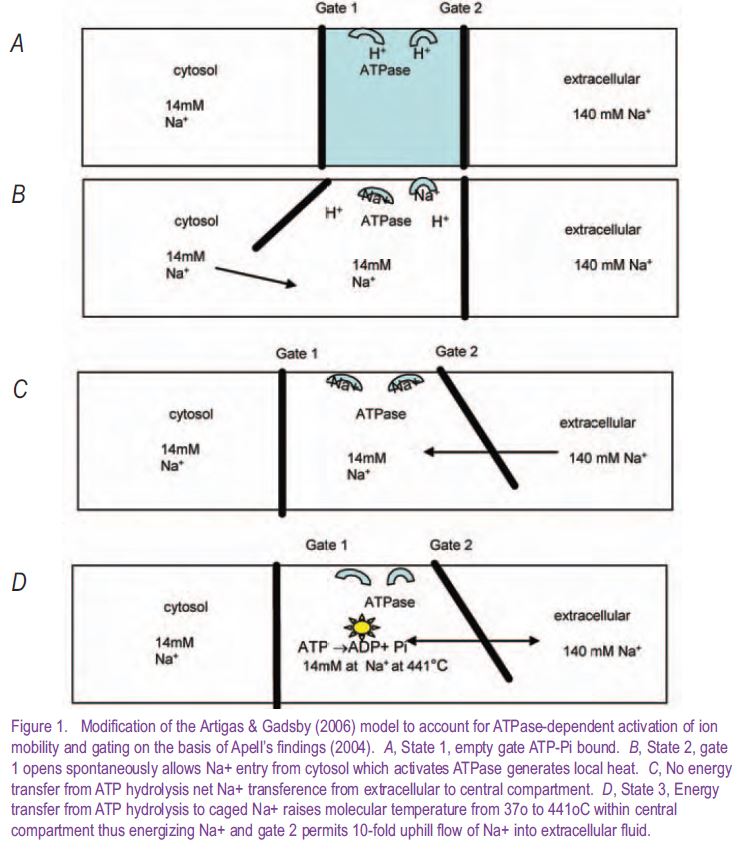
Normally, in isothermal isobaric conditions, it is assumed that ligand thermodynamic activity is controlled exclusively by changes in electrochemical potential. However, in an enclosed chamber such as envisaged between the gates of the P-ATPase, it is possible for thermal energy to be transferred from the exothermic reaction of ATP hydrolysis to increase the local activity of mobile ligands within the cage. The local scalar chemical reaction will provide a vectorial pump drive if polarized selective escape mechanisms for K+ and Na+ are available via the gates.

For net uphill Na+ movement, from the cage, through the gate, into the trans (external) solution, where the ligand reaches a steady state concentration ≈10-30 fold higher (140mM) than in the cis solution (14mM), requires an equivalent increase in kT energy of the transported molecule sufficient to raise the ‘temperature’ within the central cage from 37°C to 441°C .

To obtain energetic equivalence between the caged ions Na+1 and those in the external solution at higher concentration Na+2,

RT1a Ln Na+1 = RT2 Ln Na+2

the temperature of Na+1 has to be raised to T1a

Hence, if Na+2/ Na+1 = 140 mM/14 mM and T2 = 310°K, then T1a = 714°K.

Assuming the occluded compartment has a spherical volume with radius ≈ 3-4 Å, then hydrolysis of 1 molecule of ATP ≅ 83 zJ (1 zeptoJoule = 10-21J) will generate sufficient heat to power net Na+ diffusion ‘uphill’ against of 30-fold concentration gradient. Given a thermal conductivity of 0.6 W/m/°K, a density of 1000 kg/m3 and heat capacity of 4 kJ/°K/kg, this heat would be dissipated over a distance of 1 nm in ≈ 5- 10 ps.

Problem with secondary active transport

The early papers on cotransport clearly differentiated between its kinetic and thermodynamic elements (Heinz & Patlak, 1960; Vidaver & Shepherd, 1968). The law of mass action requires rate equations describing ligand movements of Na+ and any organic solute G, complexed to a carrier (Na2.G.C); where n Na+ atoms and one molecule, G, are bound to the carrier (C), that there will be separate term(s), kij ∝ [Na]n and [G] and ([Na]n. [G]) within the rate equation.

Even if it assumed that the only mobile carrier forms are (Na+2.G.C) and C within the membrane phase, the thermodynamic work done to transport Na+ and G between the solutions bathing each side of the membrane relates only to the chemical, or electrochemical potential differences of the ligands existing between the external solutions, where the ions and solute G remain totally dissociated. The external work ∆W done in transporting ligands Na+ and G from the left solution (l) to the right solution (r) across the membrane is:

∆W = RT Ln ( Nal /Nar ) + F∆E + RT Ln (Gl /Gr )+ RT Ln ( JNarl /JNalr )+ RT Ln ( JGrl /JGlr ) – ∆Φ

Jilr is the flux of component i, from left to right side (mole.cm-2 s-1) and ∆Φ is the work dissipated in irreversible losses, F is the Faraday constant and ∆E the transmembrane potential, R is the gas constant, T temperature degrees Kelvin, G the concentration of glucose inside or outside.

When the concentrations of transported ligand (glucose) rises in the internal solution, so that the net glucose flux tends to zero, a steady state will be reached and in Kimmich’s words ‘for a transport system entirely driven by the transmembrane potential difference in the electrochemical potential for Na+ the following relationship must be obeyed’ (Kimmich, 1981):

RT Ln ([Gi]/[Go]) ≤ (RT Ln ([Na]o/[Na]i) + F∆E)n

This ‘thermodynamic’ mechanism with assumptions of equality of thermodynamic driving forces controlled by a fixed stoichiometric coefficient ‘n’,  where n is an integer between 1 and 4, quickly acquired mechanistic significance. In chicken enterocytes, the accumulation ratio inside/outside of 3-O methyl-D glucose >70 for a Na+ gradient of approximately outside/inside = 10. It was deduced that the thermodynamic potential driving uphill intracellular sugar accumulation requires the stoichio-metric coefficient n ≅ 2 moles Na+ per mole of sugar and carrier:

e.g. [Glucose] in / [Glucose] out = [Na] 2 out / [Na] 2 in

The carrier model of cotransport assumes that no significant energy loss within the carrier transport process and that no accompanying leak of uncomplexed ligand occurs, irrecoverable work = ∆Fx = 0 and n is the ‘stoichiometric coefficient of Na+ binding within the mobile carrier complex. In theory, at static head, no net flux of either the driving solute Na+, or the driven solute glucose occurs. Any leaks that do occur i.e. uncoupled Na+ or glucose movements and even in the isolated transporter they do (Parent et al. 1992, Loo et al. 1998) are assumed to be outside the cotransport process and can be factored out of the central assumption of the cotransport model- that there is a static complex between the mobile ligands and carrier lasting the duration of passage across the transporter.

Another way of viewing cotransport is by use of the phenomenological equations originated by Onsager (1931):

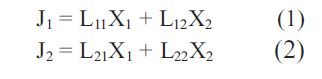
In this case J1 represents Na+ flux via a membrane containing Na+ glucose cotransporters and X1 is the conjugate driving force of Na+, the electrochemical potential gradient of Na+ = (RT Ln ([Na+] out/[Na+] in) + F ∆ψ); Lii are straight coefficients defining the linear relationship between the driving forces Xi and their conjugate flows Ji. J2 represents glucose flow via the Na+ -glucose cotransporter within a brush-border membrane, its conjugate force X2 = RTLn ([G] out / [G] in) and L22 is the straight coefficient relating glucose flow to its chemical potential gradient. The cross coefficients L12 and L21 relate the flows J1 and J2 to their non-conjugate forces i.e. X2 and X1 respectively.

If glucose accumulates on one side to an extent where net glucose movement

= J2 = 0,
Then in equation 2: where
J2 = 0, i.e. the static head for glucose transport;

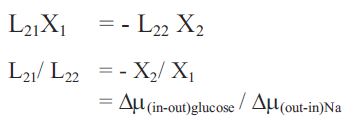
The ratio of thermodynamic forces X2/ X1 = ∆µglucose/ ∆µNa between the internal and external solutions for glucose and between the external and internal solutions for Na+ is similar to the stoichiometric coefficient ‘n’, as defined by Kimmich. However, this phenomenological treatment, unlike that of Kimmich, requires no assumptions about the constancy of n, or that at static head that both JNa = Jglucose = 0. Equations 1 and 2 indicate that the static head condition only applies to the driven solute (glucose) and continuous leakage of the driving solute, Na+ is a necessity, rather than an irrelevant inconvenience.

The extent of glucose accumulation at static head relates directly to the cross coefficients, Lij, which in turn relate to the frictional interactions between Na+ and glucose within the transporter. The thermodynamic forces in the external solutions driving Na+ and glucose transport are unaltered by the extent of Na+-glucose interaction within the transporter and may explain why Na+ leak current across SGLT1 is reduced by glucose (Loo et al. 1998; Parent et al. 2000).

A perceived disadvantage of phenomenological equations is their generalized nature: no mechanism other than a frictional interaction is specified and is therefore considered to be too vague to be useful – in contrast to the highly specific cotransporter models. However, the phenomenological equations have the advantage of transparency in illustrating the underlying physical principles governing coupling.

Alternative models for cotransport in which direct energy transference within a pore-like transporter between adjacent molecules have been postulated (Hodgkin & Keynes, 1955; Su et al. 1996; DeFelice, Adams & Ypey, 2001). These alternative mechanisms gives reasonably satisfactory simulations of the observed data both for Na+- 5HT cotransport and Na+-glucose transport.

Collision models have the major advantage that they do not make assumptions about large protein conformational changes, allow for dissipative losses (leaks) to generate the flows, and are more consistent with the known structures of biological transporters.

Acknowledgement

This article was prepared as the result of discussions with Louis J DeFelice (Department of Physiology, Vanderbilt University, Nashville, TE, USA). An excerpt is included in the supplement to his recent review DeFelice LJ & Goswami T (2007). Transporters as channels. Annu Rev Physiol 6, 87-112.

References

Apell HJ (2004). How do P-type ATPases transport ions? Bioelectrochemistry 63, 149-156.

Artigas P & Gadsby DC (2006). Ouabain affinity determining residues lie close to the Na/K pump ion pathway. Proc Natl Acad Sci USA 103, 12613-12618.

Boyer PD (1997). The ATP synthase–a splendid molecular machine. Annu Rev Biochem 66, 717-749.

Crane RK (1962). Hypothesis for mechanism of intestinal active transport of sugars. Fed Proc 21, 891-895.

Curran P F (1960). Na+, Cl- and water transport in rat ileum in vitro. J Gen Physiol 43, 1137-1148.

DeFelice LJ, Adams SV & Ypey DL (2001). Single-file diffusion and neurotransmitter transporters: Hodgkin and Keynes model revisited. Biosystems 62, 57-66; 70, 762-767

Edwards C & Harris EJ (1957). Factors influencing the sodium movement in frog muscle with a discussion of the mechanism of sodium movement. J Physiol 135, 567-580.

Garrahan PJ & Glynn IM (1967). The stoicheiometry of the sodium pump. J Physiol 192, 217-235.

Harmel N & Apell HJ (2006). Palytoxin-induced effects on partial reactions of the Na,K-ATPase. J Gen Physiol 128, 103-118.

Harris EJ (1957). Permeation and diffusion of K ions in frog muscle. J Gen Physiol 41, 169-199.

Heinz E & Patlak CS (1960). Energy expenditure by active transport mechanisms. Biochim Biophys Acta 44, 324-334.

Hodgkin AL & Keynes RD (1955). The potassium permeability of a giant nerve fibre. J Physiol 128, 61–88.

Homareda H, Nagano Y & Matsui H (1991). Interaction of sodium and potassium ions with Na+,K(+)-ATPase. IV. Affinity change for K+ and Na+ of Na+,K(+)-ATPase in the cycle of the ATP hydrolysis reaction. J Biochem 109, 70-77.

Jardetzky O (1966). Simple allosteric model for membrane pumps. Nature 211, 969-970.

Kedem, O (1961). Criteria of active transport. In Membrane transport and metabolism: proceedings of a symposium held in Prague, August 22-27 1960, ed. Kleinzeller A& Kotyk A, pp 87-93. Academic Press, London.

Kedem O & Katchalsky A (1961). A physical interpretation of the phenomenological coefficients of membrane permeability. J Gen Physiol 45, 143-179.

Kimmich GA (1981). Gradient coupling in isolated intestinal cells. Fed Proc 40, 2474-2479.

Lauger P (1984). Thermodynamic and kinetic properties of electrogenic ion pumps. Biochim Biophys Acta 779, 307-341.

Lew VL, Glynn IM & Ellory JC (1970). Net synthesis of ATP by reversal of the sodium pump. Nature 225, 865-866.

Ling GN & Ochsenfeld MM (1976). Na+ and K+ levels in living cells: do they depend on the rate of outward transport of Na+? Physiol Chem Phys 8, 389-395

Loo DD, Hirayama BA, Gallardo EM, Lam JT, Turk E & Wright EM (1998). Conformational changes couple Na+ and glucose transport. Proc Natl Acad Sci USA 95, 7789-7794.

Mitchell P (1977). Vectorial chemiosmotic processes. Annu Rev Biochem 46, 996-1005.

Murer H & Hopfer U (1974). Demonstration of electrogenic Na+-dependent D-glucose transport in intestinal brush border membranes. Proc Natl Acad Sci USA 71, 484-488.

Onsager L (1931). Reciprocal relations in irreversible processes. Phys Rev 37 405-426.

Parent L, Supplisson S, Loo DD & Wright EM (1992). Electrogenic properties of the cloned Na+/glucose cotransporter: I Voltage-clamp studies. J Memb Biol 125, 49.

Post RL & Jolly PC (1957). The linkage of sodium, potassium, and ammonium active transport across the human erythrocyte membrane. Biochim Biophys Acta 25, 118-128.

Skou JC (1998). Nobel Lecture. The identification of the sodium pump. Biosci Rep 18, 155-169.

Stock D, Gibbons C, Arechaga I, Leslie AG & Walker JE (2000). The rotary mechanism of ATP synthase. Curr Opin Struct Biol 10, 672-679.

Su A, Mager S, Mayo SL & Lester HA (1996). A multi-substrate single-file model for ion-coupled transporters. Biophys J 70, 762-777.

Ussing H H & Zerahn K (1951). Active transport of sodium as the source of electric current in the short-circuited isolated frog skin. Acta Physiol Scand 42, 298-308.

Vidaver GA & Shepherd SL (1968). Transport of glycine by hemolyzed and restored pigeon red blood cells. Symmetry properties, trans effects of sodium ion and glycine, and their description by a single rate equation. J Biol Chem 243, 6140-6150.

Whittam R & Ager ME (1964).Vectorial aspects of adenosine-triphosphatase activity in erythrocyte membranes. Biochem J 93, 337-348.

Whittam R & Ager ME (1965). The connexion between active cation transport and metabolism in erythrocytes. Biochem J 97, 214-227.