https://doi.org/10.36866/pn.111.38

Electrochemical signalling allows rapid communication between neurons to coordinate sensory information and the responses of billions of cells around the body. Students are taught that these electrical nerve impulses, or action potentials, propagate through local changes in potential difference along the cell membrane caused by the opening of ion channels, which in turn trigger neighbouring voltage-sensitive ion channels to open, and so forth, like a set of dominoes. Here, we reconsider the fundamental nature of action potentials and whether their generation may also involve a pulsatile mechanical element arising from ion channel opening and subsequent transmission of kinetic energy through the lipid bilayer via a ‘soliton’ (a self-reinforcing solitary wave packet that maintains its shape while it propagates at a constant velocity).

The Hodgkin and Huxley (H&H) action potential model described in 1952 predicts the nature of ionic currents crossing cell membranes which creates a potential difference that changes over time due to changes in the ionic equilibrium. It is well supported by electrophysiological measurements and observations. Recent evidence suggests that a “force-from-lipid” model (Brohawn et al., 2014) could transmit pulses into mechanosensitive ion channels in the absence of other cellular components and might also explain propagation through the membrane lipid. We envisage that it would take the form of a soliton known as an action potential pulse (APPulse) which would be the precursor of ion channel opening. Action potentials are critical to the operation of the brain and computation and timing of the action potential is important in considering any possible computational requirements. This is particularly true when striving to model artificial intelligence (AI) where accurate coding and timing of action potentials are paramount.

Action potential models and mechanisms in AI must correlate with perceived observations and incorporate physical elements to accurately reflect the movement of ions and action potential spread across the entirety of the cell membrane. Thus, the mechanisms that define the speed of the action potential will directly affect the available methods of reliable computation available to an artificial brain neural network where changes in accuracy of action potential timing would make any form of computation unreliable. Therefore, it is important when considering the action potential to consider the standpoint from which it is viewed.

The physiological viewpoint

Measurements taken of the action potential are taken from both sides of the membrane and measure the potential difference across a wide area – this is the macroscopic view. Electrophysiologically, ‘patch clamp’ studies may assess areas of membrane at the microscopic level when examining single or at least a limited number of ion channels.

An action potential may be measured with intracellular microelectrodes in continuum with the cytosol – but is a product of the ion changes at the surface of the membrane. Small diameter axons (approx. 0.2 µm) have low concentrations of widely spread ion channels (Holden and Yoda, 1981; Catterall, 2012). Patch clamp studies can measure the potential changes at the membrane but cannot measure live action potentials. As the action potential progresses the micro-pipette measures current not from a point on the membrane, but from a temporally adjusted area including multiple ion channels, and may not reflect the mechanisms of propagation from a single point.

The Hodgkin Huxley equation and Cable Theory

The Hodgkin Huxley equation and Cable Theory.  The H&H equation describes ionic flow across the membrane in mathematical terms over the time period between when the membrane reaches threshold and the end of the refractory period. At any one point on the membrane at any moment the polarity can be thought of as being in one of three states: resting, polarised or refractory. The membrane can be considered polarised immediately before the threshold takes effect, as after that point there is no return. After threshold the membrane is in the refractory state as no further action potential can be created without a return to the resting state.

The action potential typically has a maximum speed of ~ 1 m/s in unmyelinated axons (Waxman and Bennett, 1972).  We know therefore that there is a ‘leading edge’ just before depolarisation and that, in order to advance the action potential, this leading edge must have the innate property of self-propagation. In effect, the leading edge also instigates the refractory period once the depolarizing wave has passed. Patch clamp recordings of single ion channels have demonstrated that threshold, the depolarisation spike and the refractory period can all be explained by the movement of Na⁺ through its channel alone (Holden and Yoda, 1981; Catterall, 2012). Thus, the physical origins of the potential changes associated with the action potential can be directly attributed to the ion channel mechanisms, with the activity of the Na⁺ channels defining its progression.  This implies that the only element of the action potential that is responsible for its live propagation is defined by the mechanism that causes the threshold at the leading edge. The threshold alone is the initiator of the action potential and the rate limiter to the speed of the action potential. The action potential over a given surface is temporally stable and, for example, in the small neurons of the cortex timing differences are accurate to under a millisecond.

The timing of the spike is therefore directly related only to the threshold. The threshold may be better defined temporally so that it is not a potential difference but a change over time. The rest of the action potential is only concerned with the refractory period and stabilisation to resting potential and is irrelevant to speed of transmission, although of course the refractory period can affect the frequency of transmission.  All of the above should be fairly obvious to neurophysiologists.

The physical and biophysical viewpoint

As above, the mechanism that defines the threshold can be investigated with the knowledge of the properties of just the Na⁺ channels and the membrane.  Cable Theory defines the potential arising from ion disparity across the membrane acting as a capacitance.  Historically Cable Theory comes from a direct analogy from capacitance theory and considers charge over the whole surface of an insulator.

The depolarisation of the membrane during the action potential is analogous to the discharge of a charged capacitor and the mathematics of cross current resistances appear to work correctly over a large part of the membrane in the macroscopic view experimentally. This is the basis for the H&H model. A capacitor charging under voltage clamp therefore acts as expected as the potential changes, as each measurement is independent of time.

In an electrical capacitor the change of charge is due to electrons. The charge of an electron is not fixed to its atom and charge at any place on the plate surface rises immediately. The same charge may be measured at any location on the surface; because it is charge that is created rather than current, there is always spread of potential from one site on a plate to the other. During charging this occurs when electrons align, and is a time dependent process, subject to the lateral resistance of the plate. Electrons have the ability to spread their charges freely and are not fixed by location since they are freely distributed and, importantly, charge is evenly spread along the insulator.

When H&H were conducting their experiments an accurate depiction of the membrane, ion channels and specifically inter-channel distances was not available and channels were assumed to be “separated by an infinitesimal distance”. It was not until the 1970s-80s when single patch clamping became available (Hamill et al, 1981) that accurate measurements of channel density became known (Hille, 1992). At the time that H&H described longitudinal flow the assumption was that there was a mechanism by which activation of an ion channel during threshold would activate adjacent ion channels and produce a cumulative and on-going propagation – just as the charging electrons distribute evenly and almost instantaneously. However, the mechanism of propagation between channels was not identified then and has still not been identified today.

The action potential does not take place across the whole neuron or axon at once, but travels across the neuronal membrane. By the time a propagating action potential is measured by a pipette from the interior of the axon the threshold of the action potential has already passed and the resulting measurement is a result of all the combined ionic changes over a very wide portion of membrane. The observed action potential results from the imbalance of positive ions across the membrane and during voltage clamp induced steady state these may be predicted from the H&H model.

Intra-ion channel distances have been measured accurately although this distance is variable. Single (or low multiple) ion channel recording using a patch clamp pipette of   ̴1.5 µm diameter is reliant on a low density of ion channels within the isolated membrane ‘patch’. As the membranes examined contain many different ion channels we can confidently say the Na+ channels are spaced at least 1.5 µm apart otherwise two channels are detected. As Hille (1992) points out “channels are not crowded” together and the distance a Na⁺ ion has to affect another is limited by the time taken to travel through the ion specific channel and to the next channel. The ionic radius of Na⁺ is known and is about 116 picometres (Shannon, 1976) indicating that a Na⁺ ion has to lie adjacent or in very close proximity to the Na⁺ channel. The time required for charge to spread from one ion channel to the next can be calculated from the ionic radii and the diffusion coefficient (Goodman et al., 2005). A conservative simple Speed-Time calculation suggests that the maximum speed Na⁺ ions can travel between channels is less than a thousandth  of what is necessary for propagation (Johnson, 2015).  Cable Theory only models the ion flows of the action potential under conditions of voltage clamp, but as yet there is no known mechanism for propagation of the action potential provided by Cable Theory.  This suggests that the H&H model only demonstrates the electrically measured activity surrounding the underlying mechanism of propagation from one channel to the next, not the mechanism itself.

Is there evidence for a mechanical component in action potential propagation?

For propagation to occur positive ions (i.e. Na⁺) would have to behave as electron-like particles for the diffusion kinetics to make sense. Therefore, without a mechanical component the H&H action potential cannot propagate.

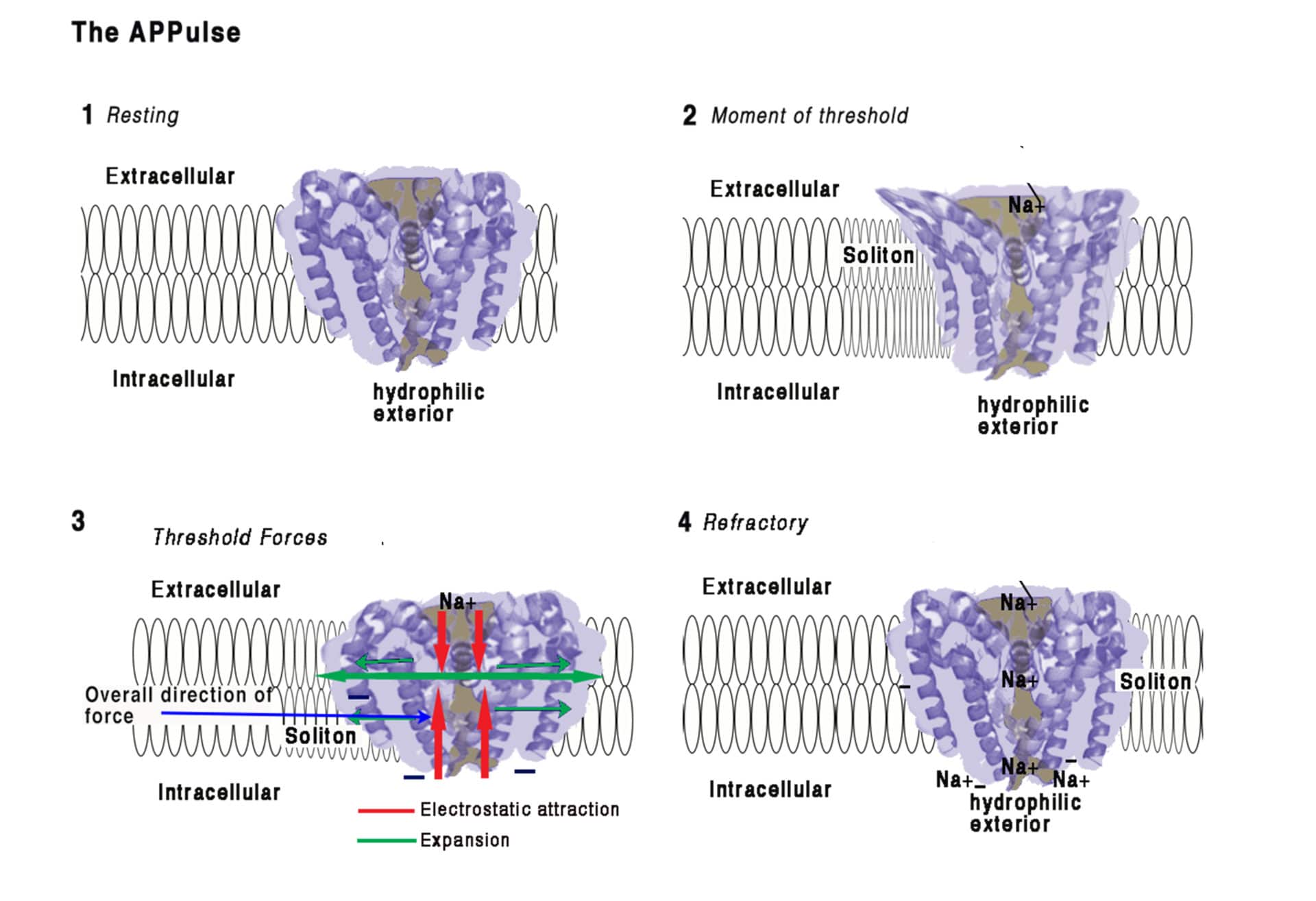
As mentioned above, the “force-from-lipid” model (Brohawn et al., 2014) could also explain propagation through the membrane lipid, via a soliton mechanical lipid pulse which is coupled to forces created by the electrostatic opening of ion channels (Figure 1). A substantial body of evidence supports the APPulse concept (Table 1).

The action potential measured by H&H is a measure of the sum of all the potential changes of all charges across the membrane over a wide area. There is a timing dissonance for the observer where the latency caused by the pipette creates the impression of a combined effect of all the ion channels over a large period of time. The result is always a combination of effects from many ion channels, some open, some closed and some inactivated and thus contributing to the refractory period of the action potential.

Positive ions do not behave as electrons and require time and the correct diffusion coefficient to move. Calculation of ion channel distribution from single channel studies, demonstrates that Cable Theory can only account for the action potential in its stable states (resting or maintained by voltage clamp) (Takahashi et al., 2016), but the ion channels are spread too far apart for the H&H model to work. The longitudinal resistance in the H&H arrangement is always infinite as there is no mechanism that provides surface spread depolarisation. Surface spread and thus speed of action potential must therefore occur by another mechanism – the APPulse suggests that this is by a mechanical ‘soliton’ wave coupled to entropy provided by the ion exchangers described (Takahashi et al., 2016).

A deconstruction of the action potential yielded evidence for a synchronised oscillating pulse structure energetically derived from the ion exchange mechanisms (Hodgkin and Huxley, 1952; Takahashi et al, 2016) and a subsequent mechanical pulse. Such a pulse mechanically opens ion channels leading to further depolarisation (Takahashi et al., 2016). This model can also help to explain action potential transmission in myelinated nerve. The pulse could be controlled by the ion channels because if there are insufficient ion channels to produce enough  energy for the pulse to reach the channels at the next node of Ranvier, then it will fail as in ion channel blockade.

Therefore, the action potential travels at a speed commensurate with the membrane dynamics of the axon: the transmission dynamic of any axon or part of an axon may be different depending upon the membrane components and the physical formation of the membrane. At any time the transmission dynamic represents the exact state of the axon and everything that affects its transmission timing, speed and refractory state. Speed of axonal transmission, and therefore the time impulses take to reach their destination, is variable and depends upon the axon type and diameter.

Conclusion

The action potential as expressed by Hodgkin and Huxley (1952) is a measurement of the progression of ionic charge over the axon membrane, but it cannot represent the mechanism of propagation. This is because the physical properties of Na⁺ ions cannot allow flow of charge from one ion channel to the next in the time available.  There must therefore be another mechanism present and we propose that this is provided by a ‘soliton’ mechanical pulse, which is the force-from-lipid mechanical force that opens the Na⁺ channels.  This coupled APPulse fulfils the requirement for a continuing action potential where Cable Theory fails.

References

Anishkin, A, Loukin, SH, Teng, J and Kung, C (2014). Feeling the Hidden Mechanical Forces in Lipid Bilayer Is an Original Sense. PNAS 111, 7898–7905.

Brohawn, SG, Zhenwei S, and MacKinnon R (2014). Mechanosensitivity is mediated directly by the lipid membrane in TRAAK and TREK1 K⁺ channels. PNAS 111, 3614-3619.

Catterall WA (2012). Voltage-Gated Sodium Channels at 60: Structure, Function and Pathophysiology. J. Physiol. 590, 2577–2589.

Goodman, JA, Kroenke, CD, Bretthorst, GL, Ackerman, JJH and Neil JJ (2005). Sodium Ion Apparent Diffusion Coefficient in Living Rat Brain. Magnetic Resonance in Medicine 53, 1040-1045.

Hamill, O. P., Marty, A., Neher, E., Sakman, B. and Sigworth, F. J. (1981). Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Archiv 391, 85-100.

Hille B (1992). Ion Channels of Excitable Membranes. Sunderland, Mass.: Sinauer.

Hodgkin AL and Huxley AF (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500-544.

Holden AV and Yoda M (1981). The effect of ionic channel density on neuronal function. J. Theor. Neurophysiol. 1, 60–81.

Howarth, JV, Keynes, RD and Ritchie, JM (1968). The origin of the initial heat associated with a single impulse in mammalian non-myelinated nerve fibres. J. Physiol 194, 745-793.

Johnson AS (2015). The Coupled Action Potential Pulse (Appulse)–Neural Network Efficiency from a Synchronised Oscillating Lipid Pulse Hodgkin Huxley Action Potential. EC Neurology 2, 94-101.

Machta, B., and El Hady A (2015). Mechanical surface waves accompany action potential propagation.” Biophysical Journal 108, 206a-207a.

McCusker, E., Bagnéris, C., Naylor, C., Cole, A., D’Avanzo, N., Nichols, C. and Wallace, B. (2012). Structure of a bacterial voltage-gated sodium channel pore reveals mechanisms of opening and closing. Nature Communications, 3:1102.

Shannon RD (1976). Revised Effective Ionic Radii And Systematic Studies Of Interatomic Distances In Halides And Chalcogenides”. Acta Crystallographica Section A, 32, 751-767.

Shen, H., Zhou, Q., Pan, X., Li, Z., Wu, J. and Yan, N. (2017). Structure of a eukaryotic voltage-gated sodium channel at near-atomic resolution. Science, 355, eaal4326.

Takahashi K, Matsuda Y and Naruse K (2016). Mechanosensitive ion channels. AIMS Biophysics, 3, 63-74.

Tasaki I and Byrne PM (1992). Heat production associated with a propagated impulse in bullfrog myelinated nerve fibers. Jap. J. Physiol. 42, 805-813.

Waxman, S. G. and Bennett, M. V. L. (1972). Relative conduction velocities of small myelinated and non-myelinated fibres in the central nervous system. Nature New Biology 238, 217-219.