Rong Zhang, Shayla Derousseau, Benjamin D. Levine
Institute for Exercise and Environmental Medicine, Texas Health Presbyterian Hospital Dallas, UT Southwestern Medical Center at Dallas, TX, USA

https://doi.org/10.36866/pn.76.9

In this study, transfer function gain (reflecting the strength of association between blood pressure and cerebral blood flow) and phase (reflecting the timing of association) were reduced during acute increases in arterial pressure induced by phenylephrine infusion. Windkessel model simulation suggested that oscillations in brain blood flow are modulated not only by dynamic autoregulation, but also by changes in steady-state cerebrovascular resistance and/or vascular compliance.

The brain has a high metabolic rate, and brain perfusion is vital for neuronal function and survival. Under resting conditions, the human brain receives about ~15–20% of the cardiac output. This demand for blood supply is so imperative that only a few seconds of ischaemia is sufficient to derange brain function profoundly and can result in syncope. Based on the Fick principle, Kety and Schmidt measured brain blood flow for the first time in humans over 50 years ago by using a diffusible inert gas (N2O) method (Kety & Schmidt, 1945). With the classic Kety–Schimdt method, only whole brain perfusion can be measured and it takes about 10 min to complete one measurement. Over the years, the technology for measuring brain blood flow has been improved substantially. At present, regional brain blood flow can be measured with a spatial resolution of several millimeters and a temporal resolution of about 1 min by using positron emission tomography (PET) or magnetic resonance imaging (MRI).

Measuring brain perfusion with high spatial and temporal resolution is important because brain perfusion is heterogeneous and dynamic. In this regard, the development of transcranial Doppler (TCD) in the early 80’s has provided a powerful tool for measuring dynamic changes in brain blood flow in the basal cerebral arteries with a high temporal resolution of about 10 ms (Aaslid et al. 1982). Using TCD, pulsatile changes in brain blood flow in response to pulsatile changes in arterial pressure can be recorded continuously on a beat-to-beat basis. Our earlier work demonstrated that mean cerebral blood flow (CBF) velocity averaged within each cardiac cycle fluctuates spontaneously with various amplitudes over many time scales. In addition, these beat-to-beat fluctuations in CBF velocity are similar to the observed changes in arterial pressure (Fig. 1) (Zhang et al. 2000). Assuming that the diameter of basal cerebral arteries (conduit arteries) remains constant, changes in CBF velocity represent beat-to-beat changes in brain blood flow. Notably, the magnitude of spontaneous oscillations in CBF velocity can be as large as 30% of its mean value even under resting conditions, which highlights the dynamic nature of brain perfusion (Fig. 1) (Zhang et al. 2000).

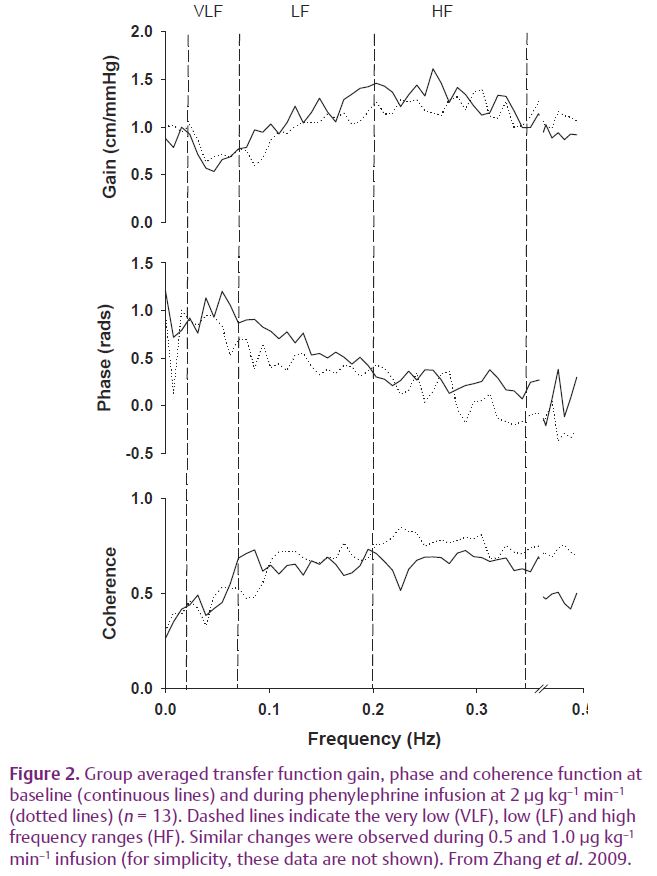
However, these observations appear to be at odds with the prevailing concept of cerebral autoregulation which states that brain blood flow remains relatively constant in spite of large changes in arterial pressure. This paradox between the traditional concept of cerebral autoregulation and the observed large oscillations in CBF velocity may be explained by the limitations of previous studies for measuring CBF. With poor temporal resolution, CBF responses to dynamic changes in arterial pressure could not be revealed. The following questions then need to be answered: how should the dynamic pressure–flow relationship of the cerebral circulation be quantified, and what are the underlying mechanisms for controlling brain blood flow in response to dynamic changes in arterial pressure. To address these questions, we have demonstrated that the relationship between beat-to-beat changes in arterial pressure and CBF velocity can be quantified by using the transfer function method based on Fourier spectral analysis (Zhang et al. 1998). Briefly, we use this method to quantify how each of the frequency components of changes in arterial pressure is transmitted into changes in CBF velocity. Estimation of the transfer function showed that at the frequency range of 0.02 to 0.5 Hz, the dynamic pressure–flow relationship of the cerebral circulation can be described as a ‘high-pass’ filter. That is, transfer function gain is low at low frequencies and increases gradually with increases in frequency associated with a decline in phase (Fig. 2). These data have been interpreted to indicate that the ability of cerebrovascular beds to attenuate transient changes in CBF in response to changes in arterial pressure is more or less effective depending on the frequency of changes in pressure – a concept which has been referred to as dynamic cerebral autoregulation (Zhang et al. 1998).

In this study, to better understand the physiological mechanisms underlying the dynamic pressure–flow relationship of cerebral circulation, we studied the effects of acute cerebral vasoconstriction on the transfer function between changes in arterial pressure and CBF velocity in healthy young to middle-aged subjects (Zhang et al. 2009). CBF velocity was measured in the middle cerebral artery using TCD. Arterial pressure was measured either with arterial catheterization or non-invasively using Finapres. Cerebral vasoconstriction was induced by acute increases in arterial pressure with incremental venous infusion of phenylephrine. Phenylephrine is an α1-adrenoreceptor agonist, but does not have direct effects on the cerebral blood vessels since it does not pass the blood–brain barrier. Thus, cerebral vasoconstriction during phenylephrine infusion reflects mainly a vascular myogenic response to acute increases in arterial pressure.

We found that with stepwise increases in phenylephrine from 0.5 to 1.0 and 2.0 μg kg–1 min–1, mean arterial pressure averaged over a time period of 6 min increased by 11, 23 and 37%, respectively, from its baseline value of about 83 mmHg under steady-state conditions. However, CBFV increased (11%) only with the highest increase in arterial pressure. Cerebrovascular resistance index, calculated as mean arterial pressure divided by mean CBF velocity, increased progressively by 6, 17 and 23%, demonstrating effective steady-state cerebral autoregulation.

Interestingly, corresponding to cerebral vasoconstriction, transfer function gain at the low frequencies (LF, 0.07–0.20 Hz) was reduced by 15, 14 and 14%, while the phase was reduced by 10, 17 and 31%. A similar trend of changes was observed at the high frequencies (HF, 0.20–0.35 Hz), but gain and phase remained unchanged at the very low frequencies (VLF, 0.02–0.07 Hz) (Fig. 2).

We speculate that besides dynamic autoregulation, oscillations in brain blood flow in response to changes in arterial pressure also may be influenced by the steady-state increases in cerebrovascular resistance and/or vascular compliance during cerebral vasoconstriction. A three-element Windkessel model was used to test this hypothesis. The model parameters consist of central and peripheral cerebrovascular resistance and a vascular compliance component. These parameters were derived from the experimentally estimated cerebrovascular resistance index and the phase at baseline and during phenylephrine infusion.

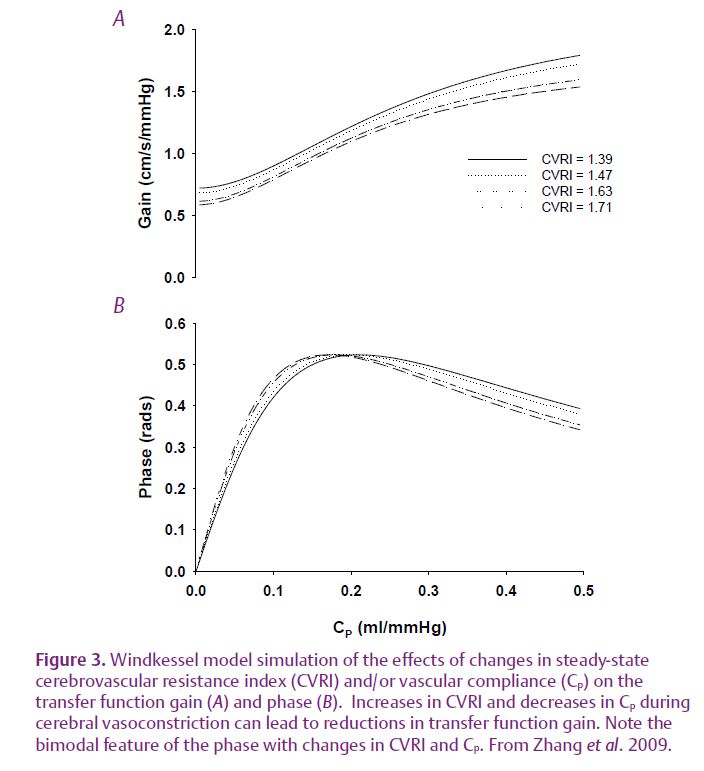
Windkessel model simulation indicates that increases in steady-state cerebrovascular resistance and/or decreases in cerebrovascular compliance (represented by the model parameter CP) can lead to reductions in transfer gain and phase (Fig. 3). Notably, the bimodal feature of changes in phase suggests that either decreases or increases in vascular compliance can lead to a reduction in phase depending on its baseline values (Fig 3).

Collectively, findings from this study suggest that changes in steady-state cerebrovascular resistance and/or vascular compliance modulate the dynamic pressure–flow relationship of the cerebral circulation at the low and high frequencies, while dynamic autoregulation is likely to be effective at the very low frequencies. Thus, spontaneous oscillations in CBF velocity, and presumably brain blood flow, are determined not only by dynamic autoregulation, but also by changes in steady-state cerebrovascular resistance and/or vascular compliance.

Spontaneous oscillations in brain blood flow or tissue oxygenation have been observed by using other brain imaging modalities such as functional MRI. There is a great interest in linking these haemodynamic changes with spontaneous brain neuronal activities to study ‘functional connectivity’. In addition, transfer function analysis of spontaneous changes in arterial pressure and CBF velocity has been used to assess dynamic cerebral autoregulation in patients with stroke, hypertension and other cerebrovascular diseases. The present study reveals the complexity of the underlying mechanisms for regulating spontaneous oscillations in brain blood flow in response to dynamic changes in arterial pressure which may provide useful information for future studies of brain perfusion in humans.

References

Aaslid R, Markwalder TM & Nornes H (1982). Noninvasive transcranial Doppler ultrasound recording of flow velocity in basal cerebral arteries. J Neurosurg 57, 769–774.

Kety SS & Schmidt CF (1945). The determination of cerebral blood flow in man by the use of nitrous oxide in low concentrations. Am J Physiol 143, 53–66.

Zhang R, Behbehani K & Levine BD (2009). Dynamic pressure–flow relationship of the cerebral circulation during acute increase in arterial pressure. J Physiol 587, 2567–2577. http://jp.physoc.org/content/587/11/2567.long

Zhang R, Zuckerman JH, Giller CA & Levine BD (1998). Transfer function analysis of dynamic cerebral autoregulation in humans. Am J Physiol 274, H233–H241.

Zhang R, Zuckerman JH & Levine BD (2000). Spontaneous fluctuations in cerebral blood flow: insights from extended-duration recordings in humans. Am J Physiol Heart Circ Physiol 278, H1848–H1855.