Paul C Pape & Karine Fénelon
Université de Sherbrooke Faculté de médicine, Québec, Canada

https://doi.org/10.36866/pn.71.31

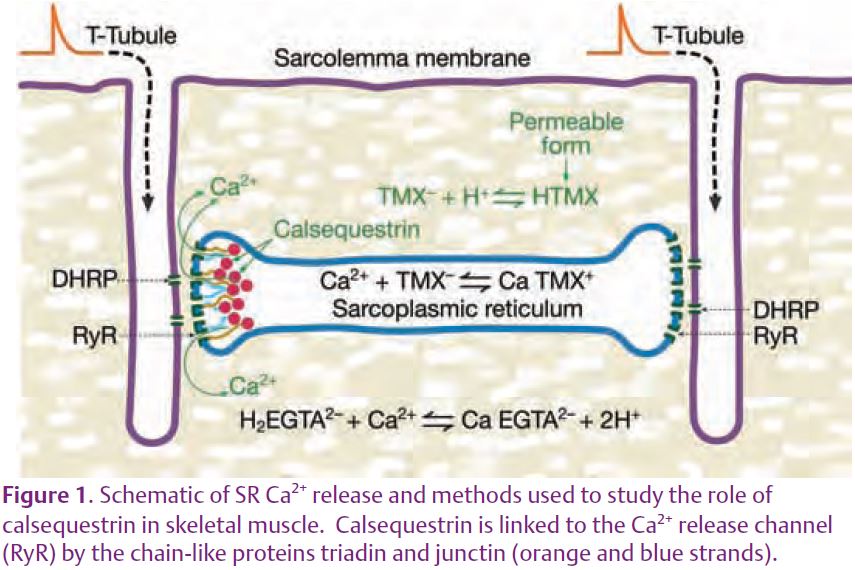
Contraction in skeletal muscle is initiated by an action potential that propagates into the centre of the fibre along invaginations of the surface membrane called T-tubules (Fig. 1). Activation of transmembrane proteins in the T-system – known as dihydropyridine receptors (DHPRs), or voltage sensors – somehow opens ryanodine receptors (RyRs) or Ca2+ release channels in the closely apposed SR membrane, probably via the physical link between the two proteins. Ca2+ released into the myoplasm activates the contractile proteins thereby causing the muscle to contract. In the junctional region, the Ca2+ release channels form a closely packed array in which every other channel is linked to a voltage sensor and the others are uncoupled. One important question in the field has been whether or not Ca2+ released from an open channel can activate neighbouring channels (uncoupled or coupled) under physiological conditions via a positive feedback mechanism known as Ca2+-induced Ca2+ release (CICR). This article reviews some recent evidence supporting this idea. It then turns to a recent study from our laboratory concerning the buffering of [Ca2+] within the SR ([Ca2+]SR) by calsequestrin. The possibility is then raised that local buffering of [Ca2+]SR by calsequestrin near open SR Ca2+ release channels could account for the apparent evidence for CICR.

With the introduction of confocal microscopy in recent years, it became possible to measure spatially-distinct, elementary Ca2+ release events termed Ca2+ sparks using fluorescent Ca2+ indicators introduced into the myoplasm. Since the density of Ca2+ sparks increases with increasing membrane voltage, each Ca2+ spark is presumably initiated with the stochastic activation of a voltage-sensor protein in the T-system and its associated SR Ca2+ release channel. The possibility of CICR was recently evaluated by comparing the flux of Ca2+ ions in Ca2+ sparks to that through single, isolated Ca2+ release channels reconstituted into artificial lipid bilayers. In a thorough analysis of Ca2+ spark data from frog fast-twitch skeletal muscle, Baylor et al.(2002) determined that an average spark produces a peak Ca2+ current of 2.5 pA. Based on two estimates of Ca2+ currents through isolated SR Ca2+ release channels in bilayer experiments of 2 pA and 0.5 pA, Baylor et al. (2002) concluded that Ca2+ sparks are composed of 1-5 SR Ca2+ release channels. One reason that the lower single-channel estimate of 0.5 pA by Kettlun et al.(2003) is probably more appropriate is that it was measured under relatively physiological conditions. This would imply that the Ca2+ sparks are composed of 5 SR Ca2+ release channels on average – one activated by its associated voltage sensor and the other 4 by CICR. Another possible interpretation, presented below, is that the Ca2+ flux is larger in Ca2+ sparks since calsequestrin –acting as a source of Ca2+ – was present, whereas calsequestrin was absent in the bilayer experiments.

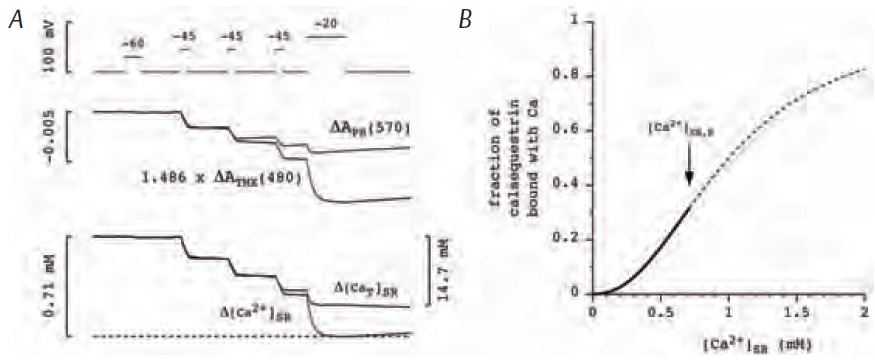
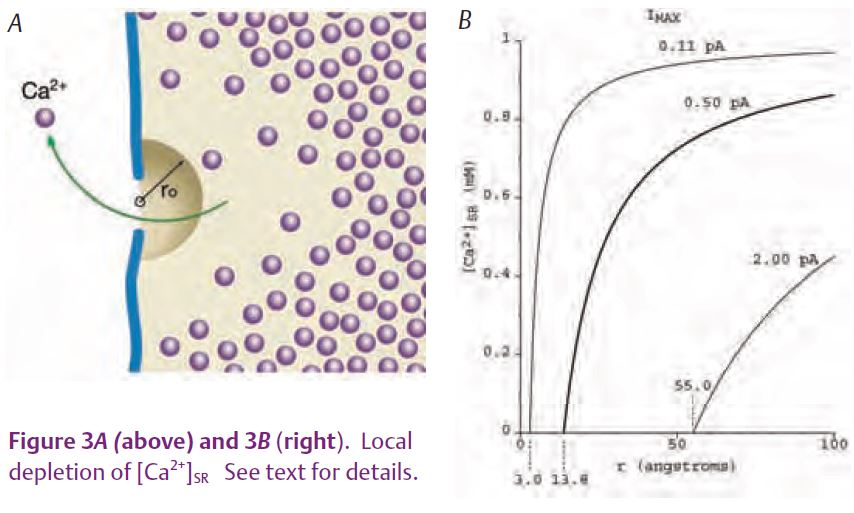
MacLennan & Wong (1971) discovered calsequestrin and proposed that it acts to buffer luminal [Ca2+] since it has such a high capacity for binding Ca. Volpe and Simon (1991) challenged this idea with their estimate that only ¼ of released Ca2+ comes from calsequestrin and the rest comes from the pool of free Ca2+ in the SR. (Calsequestrin is considered to be the source even though a Ca2+ ion has to unbind from calsequestrin and enter the pool of free Ca2+ before being released.) We recently reported on experiments in isolated fast-twitch skeletal muscle fibres aimed at resolving the Ca2+ buffering properties of calsequestrin in frog fast-twitch skeletal muscle (Pape et al. 2007). These experiments involved the simultaneous measure-ment of two optical signals: one to measure the total amount of Ca in the SR (denoted [CaΤ]SR) and the other to give [Ca2+]SR. [CaΤ]SR was measured with the EGTA/phenol red method which requires a relatively large concentration of the Ca2+ buffer EGTA and a pH indicator such as phenol red. Essentially all of the Ca2+ released into the myoplasm is rapidly captured by EGTA, which releases two protons for each Ca2+ bond (Fig.1), producing a pH change detected with phenol red. [Ca2+]SR was measured with one of the original Ca2+ indicators, tetramethylmurexide (TMX). TMX’s ability to enter and, thereby, monitor [Ca2+] in an internal compartment is most likely due to the membrane permeability of the uncharged, protonated form of TMX expected to be present in trace amounts. Owing to its low affinity for Ca2+ (KD = 2.6 mM) and the presence of 20 mM EGTA in the myoplasm, the CaTMX signal from the myoplasm should be negligible compared to that from the SR. The middle traces in Fig. 2A show the absorbance signals (ΔA) from the two indicators measured in response to the voltage-clamp stimulation shown at the top. With a reasonable assumption for the resting value of [Ca2+]SR (denoted [Ca2+]SR,R) these signals yielded the superimposed [CaΤ]SR and [Ca2+]SR signals shown at the bottom of Fig. 2A. As indicated by the calibration bars, the total amount of Ca in the SR at the start (14.7 mM) was much greater than the resting level of [Ca2+]SR (0.71 mM). This is attributable to the strong buffering by calsequestrin. An important thing to note is that the signals superimpose initially whereas the [Ca2+]SR decreases much more relative to the [CaΤ]SR later on. This indicates that the buffering action of calsequestrin is greater at the start of the stimulation when there is a physiological amount of Ca in the SR and that this ability to buffer [Ca2+]SR decreases as the SR Ca content decreases. This feature is evident in the Ca-calsequestrin binding curve derived from these results and shown in Fig. 2B. The binding curve is highly cooperative with a Hill coefficient of 2.26 in this case and about 3 on average. The slope of the curve is maximal at the resting value of [Ca2+]SR (shown by the arrow) indicating that the buffering by calsequestrin is maximal at physiological [Ca2+]SR. In summary, calsequestrin rapidly buffers released Ca2+ with greater than 20 times on average more Ca2+ coming from calsequestrin as opposed to the free pool. This result clearly indicates that calsequestrin serves to buffer the global or spatially-averaged [Ca2+]SR. We turn now to the possibility that it may also serve to prevent a local decrease in [Ca2+]SR near the mouth of an open SR Ca2+ release channel. Such a local depletion is depicted in Fig. 3A.

A starting point for assessing the possible contribution of calsequestrin is to consider what happens if calsequestrin is not present. As done previously for other ions (cf. Hille, 1968), the following analysis gives the diffusion-limited Ca2+ flux by considering an open Ca2+ release channel as a point sink located in a semi-infinite medium. [Ca2+]SR as a function of r from the mouth of the channel should rapidly (within μ secs) approach the steady-state condition given by

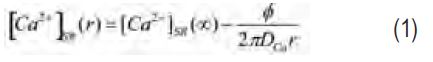
where [Ca2+]SR(∞) is the concentra-tion far from the channel, DCa is the diffusion constant for Ca2+, and φ is the flux of Ca2+ ions through the channel. (Note that this agrees with Fick’s Law since DCa times the surface of a hemisphere of radius r (2πr2) times the gradient (d[Ca2+]SR/dr) is equal to the flux, φ.) Since [Ca2+]SR cannot be negative – as would be the case if r is very close to zero – a distance r0 is introduced at which [Ca2+]SR equals zero at the diffusion-limited, maximum flux (φmax). r0 is the ‘radius of the channel mouth’ in Peskoff and Bers (1988). With this definition,

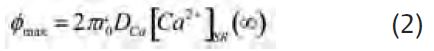
we now calculate the value of r0 corresponding to a current of 0.5 pA, the best estimate of the single-channel current above, obtained in bilayers experiments. Using Faraday’s constant (105 coulombs/equivalent), 0.5 pA corresponds to a flux of 2.5 x 10-18 moles/sec. With a value for DCa of 3 x 10-6 cm2/sec and [Ca2+]SR(∞) given by 1 mM (see Pape et al. 2007 for these parameters), the corresponding value of r0 is 13.8 Å. The diffusion gradient from equation (1) for this case – the middle and thicker curve plotted in Fig. 3B –indicates a significant amount of local depletion for distances within 100 Å from the channel. If the value for r0 of 13.8 Å is reasonable, this would indicate that the 0.5 pA single-channel current could be diffusion-limited. Hille (1968) considered a value of r0 for Na channels of 3 Å. Although apparently arbitrarily chosen, this value seems reasonable since the Pauling radius for Na is 0.95 Å. Since Ca has a similar radius, 0.99 Å, the same value of r0 might apply for the SR Ca2+ release channel. As indicated by the left-most curve in Fig. 3B, the maximum current (Imax) for this case is only 0.11 pA. This suggests that the single channel current of 0.5 pA might actually be larger than the diffusion-limited value. Likewise, the single-channel current of 2 pA above gives a value for r0 of 55 Å which seems much too large (see right-most curve in Fig. 3B) and, thus, further supports the idea above that the 0.5 pA value is more appropriate. It is possible that the single-channel current is greater than the diffusion-limited maximum owing to the presence of a net negative charge near the mouth of the channel that results from the local depletion of Ca2+. However, the maximum enhancement from this effect is only about 2-fold (cf Peskoff & Bers, 1988). Moreover, it should be significantly less in this case since the single-channel current is relatively low and since the Ca2+ release channels are significantly permeable to K+ and Mg2+ ions so that counter-ion movements of these ions into the SR would tend to reduce the net negative charge. These considera-tions indicate that the value of 0.5 pA is near, if not significantly above, the maximum single-channel current sustainable by diffusion.

A quantitative assessment with calsequestrin present is beyond the scope of this article. However, since calsequestrin has such a high Ca-binding capacity and fast kinetics, it should be able to supply Ca2+ ions thereby minimizing any local depletion of [Ca2+]SR. This could help explain the 5-fold greater current in Ca2+ sparks above compared to the single-channel current (2.5 pA vs. 0.5 pA) since only the former was determined with calsequestrin present. In summary, calsequestrin strongly buffers the spatially-averaged [Ca2+]SR. It may also serve to support relatively high single-channel Ca2+ fluxes by buffering local [Ca2+]SR near the mouth of the SR Ca2+ release channel. Calsequestrin should also serve to enhance the Ca2+ flux by introducing a negative voltage near the mouth of the channel due to negative charges on calsequestrin created when Ca2+ ions leave their binding sites.

References

Baylor SM, Hollingworth S & Chandler WK (2002). Comparison of simulated and measured calcium sparks in intact skeletal muscle fibers of the frog. J Gen Physiol 120, 349–368.

Hille B (1968). Pharmacological modifications of the sodium channels of frog nerve. J Gen Physiol 51, 199–218.

Kettlun C, Gonzalez A, Rios E & Fill M (2003). Unitary Ca2+ current through mammalian cardiac and amphibian skeletal muscle ryanodine receptor channels under near-physiological ionic conditions. J Gen Physiol 122, 407–417.

MacLennan DH & Wong PTS (1971). Isolation of a calcium-sequestering protein from sarcoplasmic reticulum. Proc Nat Acad Sci, USA 68 , 1231–1235.

Pape PC, Fénelon K, Lamboley CRH & Stachura D (2007). Role of calsequestrin evaluated from changes in free and total calcium concentrations in the sarcoplasmic reticulum of frog cut skeletal muscle fibres. J Physiol 581, 319–367.

Peskoff A & Bers DM (1988). Electrodiffusion of ions approaching the mouth of a conducting membrane channel. Biophys J 53, 863–875.

Volpe P & Simon BJ (1991). The bulk of Ca2+ released to the myoplasm is free in the sarcoplasmic reticulum and does not unbind from calsequestrin. FEBS 278, 274–278.